C.1717
Grip
Driving a car is an act of trust. You assume among other things, that the tyres and road surface will interact in a predictable way. The interaction can be pictured in terms of two forces. The first is the normal force that supports the weight of the car. The second is a shear force parallel to the road surface, and it’s the one we are concerned with here. The contact patch of a tyre has to resist sliding so that the wheel can propel the vehicle, stop it, and guide it round curves. In other words, it provides grip. If the grip fails to match the demands made on it, the car will become a projectile over which the driver has little control.
Where the grip comes from
Exactly how grip works is more complicated than you might expect. With everyday materials that you find in the home, the rules that govern how much friction is generated between two surfaces are relatively simple. There is a clear distinction between ‘static’ friction and ‘sliding’ friction. A tea plate resting on a wooden table will resist being pushed sideways, not moving until the applied force reaches a threshold value. Only then does it start to slide, and when the plate moves, the resistance falls (see Section G2016). By contrast, when the road surface applies shear force to a tyre tread (as it might when the driver applies the brakes for example), the jagged peaks in the road surface plough through the material, which deforms around them. There is a certain amount of slippage or creep, so that the distinction between static and sliding friction becomes less clear. Not only that, but the rubber tyre provides friction in two distinct ways: adhesion and hysteresis grip.
Two kinds of grip
What keeps your tea plate stationary on the kitchen table as opposed to sliding away from you at the slightest touch is adhesive friction. It is the kind of friction you are familiar with from physics at school (see Section G2016), which arises from electrical attraction between the molecules on the two surfaces. Not all of the molecules on the two surfaces take part: only a small proportion that happen to be located at ‘high spots’ scattered across the apparent area of contact. The molecules at these high spots form temporary bonds or junctions between the two materials. If you push hard enough the bonds will break and the plate will move, but new bonds will continue to form momentarily and break again as each high spot comes into contact with a new high spot on the opposite surface in a kind of ‘slip-stick’ process. The result is a shear force that continues to resist sliding motion.
Shear forces occur in pairs – the action and reaction are equal and opposite. If the table supplies a shear force that prevents the plate from moving when disturbed, the plate must at the same time exert an equal and opposite shear force on the table. A shear force can be represented diagrammatically in the form of an arrow with half of the arrowhead missing, as shown in the upper part of figure 1. Here, we see a tyre tread resting on the road surface. But the while a tea plate is rigid, the tyre tread is not. It drapes itself over each ‘asperity’ or projecting stone chip in the road surface, generating friction wherever there is contact. In figure 1, the tyre is moving from left to right, and the driver has applied the brakes, so that the tread exerts a shear force around the perimeter of the asperity (white arrows), and in return is acted upon by a complementary shear force that tends to slow down the tread (orange arrows).
Figure 1
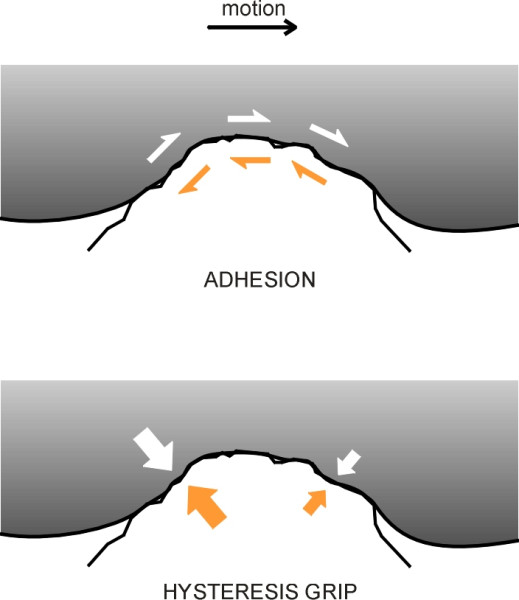
Of course, bad weather affects the adhesion between a rubber tyre and the road in the same way as it might affect any other material, because at a microscopic level, the surfaces are separated by a film of grease and water that hinders the formation of molecular bonds. What is remarkable about rubber is that the second type of grip, hysteresis grip, persists whether the road is wet or dry or even smeared with oil. To explain why, we need to look at what happens when rubber is compressed and then relaxed: in other words, what happens during a typical loading cycle.
The hysteresis loading cycle
Rubber is unusual. It can be distorted in ways that would damage other materials, and still snap back into shape. This is because of its molecular structure: long molecular chains that are coiled like tiny wire springs, but with random twists and turns so that when you stretch them, they can uncoil relatively easily. But if you stretch or squeeze a piece of rubber, not all the energy you put into the material is recovered when you let go. It exhibits hysteresis.
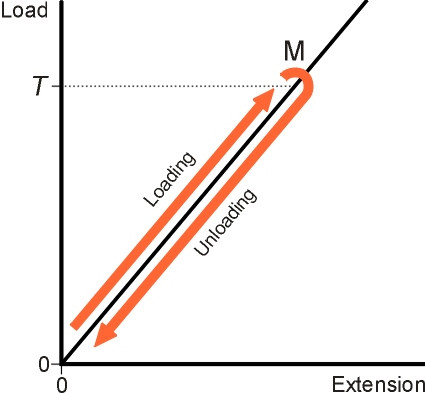
Where does the energy go? Let’s look at a ‘normal’ material first. When you pull on a steel spring, it will stretch. Denote the increase in length, the extension, by \(X\). With zero load, there is no extension (\(X = 0\)). As the load increases, the extension grows in direct proportion, the relationship following a straight line provided that the load is not too large. Let’s take it up to a target load of \(T\) kN say. Now relax the tension, but gradually. The length of the spring will fall, tracing out the original line in reverse. Crucially, the load corresponding to any particular extension is always the same, regardless of whether we are increasing the load or reducing it. In other words, the load/extension curve is identical for the two parts of the loading cycle (figure 2). In fact, we can go further. For any particular stress level, the strain will always be the same, so we could load the specimen up to twice the target value and then reduce it by 40% say, then stop for a few minutes (or years) before continuing down the target level \(T\). For a truly elastic material, the loading sequence is irrelevant.
Figure 2
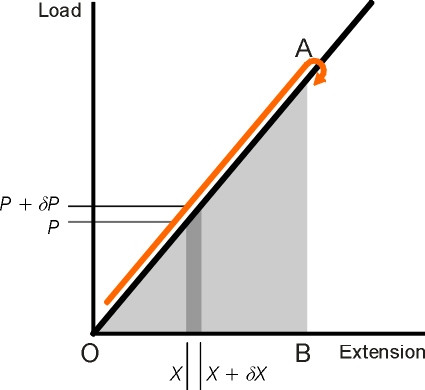
Now let’s go back to the original loading cycle. Any change in extension involves a flow of energy. During the first part of the cycle, the load is increasing (figure 3). Over any small segment of the curve, if it increases from \(P\) to \(P + \delta P\) while the extension increases from \(X\) to \(X + \delta X\), the energy put into the spring is equal to the force times distance moved, or \(P \delta X\). This increment of energy is represented by the dark grey area under the curve in figure 3, and the total energy put in during the loading process is the area of the triangle OAB. When you relax the tension in the spring, the energy flows back into your arm. Since the graph follows the same straight line back to the origin, the energy recovered is also the area under the triangle OAB. Therefore, the energy you put into stretching a steel spring is recovered when the spring is relaxed.
Figure 3
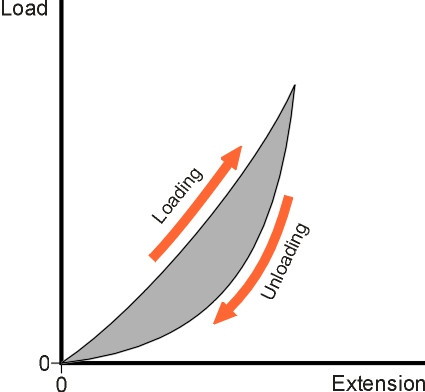
Rubber is different. It absorbs more energy during the loading process than it releases during the unloading process, as if the material were reluctant to go back to its original shape. In fact, it does recover its original shape, but the path that it follows during the unloading part of the cycle lags behind the loading curve as shown diagrammatically in figure 4. This happens because rubber molecules unravel when stretched, but side-groups of atoms attached to the chains have to be dragged past each other, which absorbs energy. This characteristic is sometimes referred to as ‘internal friction’ [5]. The energy is not recovered when the forces are relaxed as it would be with a metal, and hence the loading and unloading curves follow different paths, as shown in figure 4. The total energy lost during a loading/unloading cycle is equal to the shaded area enclosed between the two curves. This energy is converted to heat, which is why tyres get hot, especially when run at high speed. As a proportion of the total put in, it ranges between a few percent for ‘bouncy’ rubbers to 95% for ‘soggy’ ones [6], but for car tyres it is typically in the region of 50%. The proportion varies among other things with the amount of carbon filler, which is added to production car tyres in the form of fine particles. They increase the stiffness of the material, improve resistance to wear, and usually increase the hysteresis losses too.
Figure 4
The tyre tread and the road
Now we can see where hysteresis grip comes from. Unlike steel or plastic, a rubber tyre tread can mould itself to irregularities in the road surface. The jagged peaks or ‘asperities’ on the surface chippings create depressions in the tyre tread, and the sloping faces provide additional contact that wouldn’t occur with two rigid materials even when forced together under high pressure. Let us examine a single asperity. We’ll ignore adhesive friction and assume that the tyre tread exerts pressure that is everywhere at right-angles to its surface. Because the asperity is jagged, the pressure acts in various directions, many involving a significant horizontal component. On a stationary tyre, the horizontal components will balance out. There is no resultant force on the tyre tending to push it forwards or backwards along the road (see upper diagram in figure 5).
Figure 5
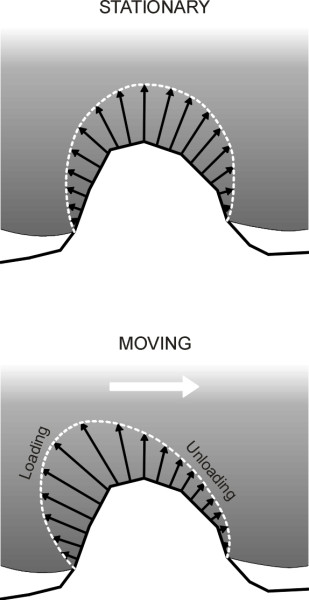
But if the vehicle is moving and the driver puts on the brakes, the inertia of the vehicle will tend to drag the tread along the road surface. You might expect this to result in increased compression along the upstream side of each peak, and reduced compression on the downstream side, by analogy with the ‘sawtooth’ model described in Section G2016. Indeed this is what happens, but there is a crucial difference: continuous deformation of the rubber surface. It is creeping along the road. As it passes over a peak, each element of rubber in the tread undergoes firstly a loading process and then an unloading process [3] [27]. The increase in pressure during the loading process is greater than the decrease during the unloading process, and the result is a net resistance (lower diagram in figure 5).
Notice that we haven’t made any reference to friction in the normal sense of the word. No shear forces are depicted in figure 5. However, as shown earlier in figure 1, shear forces will arise as the rubber flows over the asperities, with the molecules at the surface of both materials attracting one another and thereby generating resistance through conventional adhesive friction. In fact, on a dry road, the adhesion component usually accounts for the greater part of the total, and it masks the hysteresis effect. But suppose you cover the road in a layer of grease or soap so there is no molecular interaction at all. Hysteresis will still supply a coefficient of friction of around 0.4 [7] [26]. So while adhesion is badly affected when the road surface is covered by a film of water, hysteresis grip is not [9]. High hysteresis tyres are good in wet weather.
Grip and normal contact force
One of the ‘laws of friction’ that we learn at school says that the maximum friction force is proportional to the normal contact force. This is because the total area of ‘high spots’ where contact takes place increases in direct proportion to the normal force. This is approximately true for rigid materials, with the corollary that the load can be spread out over a large area or concentrated within a small one: the friction is the same (see Section G2016). But this doesn’t apply to materials such as rubber.
Why the relationship isn’t linear
One possible explanation is that when in contact with a rough surface, rubber gains some of its contact area by moulding against the sloping faces of the surface irregularities. In the case of a rubber tyre, as the wheel load increases, more of the tread squeezes into the crannies, but not in direct proportion. A great deal of extra pressure is required to force the last bit of tread into contact. Hence the hysteresis component of the friction coefficient falls away with increasing load (according to one source, the decrease is proportional to the mean contact pressure raised to the power -0.15; see [8]). Adhesion is also affected [27] and the overall result is a fall in the coefficient of friction of around 0.01 for every 10% increase in wheel load under both wet and dry conditions [10].
The gains and losses don’t balance out
The implications for rubber tyres are far-reaching. Doubling the load does not have the effect of doubling the grip, which falls short of the value that ‘classical’ friction theory would predict. Hence for rubber tyres, area matters. The larger the contact patch, the higher the coefficient of friction. Racing cars and dragsters, therefore, have ‘slick’ tyres with the widest possible tread in contact with the road. Moreover, for any given vehicle, unequal loading among the wheels represents a waste of potential grip, because the gains and losses do not balance out. For example, a significant proportion of overall grip is lost during cornering [23], because load is effectively ‘transferred’ to the outside wheels, where the increased grip does not compensate for the loss on the inner ones [19]. An obvious implication is that other things being equal, the wider the car and the lower its centre of mass, the less the load transfer and the faster it will go round corners (see Section C2009).
For the same reason, it takes longer to stop on a rough road than on a good quality road. The instantaneous load transmitted to the road surface through a moving tyre is not constant, but varies erratically above and below the static value as the wheel bounces up and down over the bumps. Because of the non-linear relationship between normal contact force and friction, grip lost on the ‘lows’ is not fully compensated by grip gained on the ‘highs’. As a result, the average retarding force can be reduced by 50% on bumpy roads [24], and the lateral cornering force similarly.
Downforce in racing
However, if you can make the car press down more heavily than it would normally do under its own weight, the grip will increase. You will then be able to brake and accelerate more sharply, and corner at higher speeds. This explains why racing car designers are concerned about ‘downforce’. Downforce is produced aerodynamically, much of it from curved plates that are essentially inverted wings mounted on the nose and tail. Fifty years ago, when aerodynamic behaviour was less well understood, it was not uncommon for the body of a sports racing car to do the opposite: generate lift (see Section C1416). At high speed on the Mulsanne straight during the Le Mans 24 hour sports car race, for example, the grip could be dramatically reduced, and drivers sometimes found it difficult to keep the car travelling in a straight line.
Handling
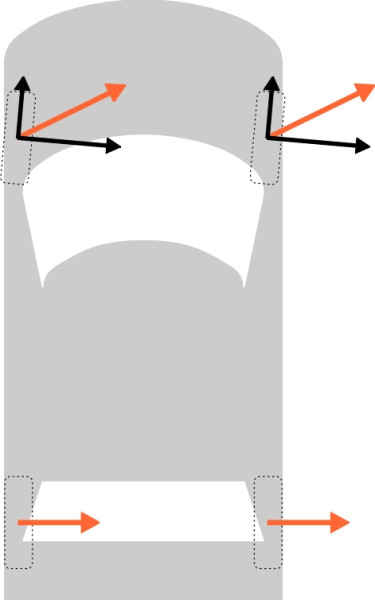
The issue of downforce brings us to a more general question: how does the tyre perform when the driver wants to corner and brake at the same time? If you are driving in a straight line, when you apply the brakes you are effectively creating a shear force that tugs rearwards on the contact patch of each tyre and slows the car down. When the car is cornering at constant speed, the force acts from side-to-side. At other times, for example when you accelerate part-way through a curve, the driven wheels undergo a combination of the two and the shear force lies at some angle in between (figure 6). In reality, there is always a mix of lateral and longitudinal forces acting on the contact patch so the direction of the resultant shear force varies from moment to moment. Hence a driven tyre must resist sliding in any direction. Grip must be available through all the points of the compass.
Figure 6
The ellipse of friction
Most tyres have roughly equal grip in all directions [16] [22], but some have less grip laterally than longitudinally. In general, if we plot the maximum value available in each direction on a diagram, we find that the points lie roughly on an ellipse centred on the contact patch as shown in figure 7. The diagram reveals something that experienced drivers know instinctively, that lateral and longitudinal grip are not independent: the total grip must be shared between them. For example, you cannot brake on a curve as hard as you might if you were travelling in a straight line because the resultant force overshoots the boundary of the ellipse. Likewise, you cannot swerve as sharply while braking as you would with your foot lifted off the brake pedal.
Figure 7
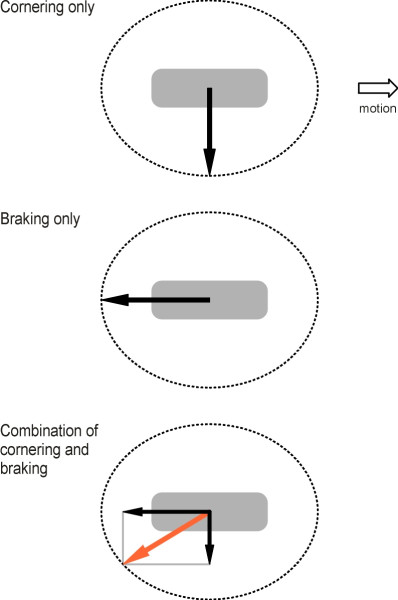
In principle, therefore, to stay in control a driver must juggle the applied forces so the resultant never strays outside the ellipse. A racing driver, on the other hand, doesn’t want to stray inside either, because this would imply surplus grip that could be exploited by some combination of braking, acceleration, or steering that would shave fractions of a second off the lap time. They include braking harder (and later) on the approach to a bend, taking the bend faster, and accelerating harder (and sooner) on the exit. All this applies mainly to the driven wheels, which on a Formula 1 car are the rear wheels. The key is to exploit the maximum grip available at every point on the circuit, so that the rear tyres operate throughout on the perimeter of the ellipse shown in figure 7. Given enough engine power, there is no respite for the tyre tread or for the driver’s neck muscles.
Tyre slip angle
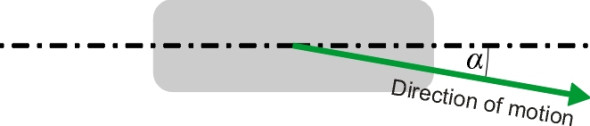
You might expect a car wheel to go where it is pointing, with its path mapped out precisely along the road as if running on a railway track. Indeed, when rolling very slowly, an upright wheel will do just that, without deviating from side to side. It has intrinsic lateral stiffness. But this stiffness falls rapidly above walking pace, becoming negligible at 20 km/h (12 mph), when a side wind will push it off course, albeit at a small angle [1]. The deviation doesn’t begin straight away, but after a short lag. The lag amounts to less than a single wheel revolution, a distance called the relaxation length [12]. In fact, in order to resist a lateral force, a tyre must point at an angle to the direction in which you want it to go (figure 8). Denoted by \(\alpha\), this angle rarely exceeds 1\(^\circ\) in normal driving, but under extreme conditions of maximum side force in a swerve it can reach 20\(^\circ\) [2]. The effect is most noticeable on the racetrack, where on high-speed corners, not only the front wheels but the whole body of a racing saloon will slewed dramatically at an angle to the direction of motion.
Figure 8
The angular difference between the direction of motion and the direction in which the wheel is pointing is known as the tyre slip angle. The phenomenon was first studied in France during the 1920’s [21]. The term ‘slip angle’ is really a misnomer [20], because the tyre doesn’t actually slip across the road surface. What happens is a combination of creep and distortion. Creep is the flow of the tread over asperities in the road surface on an almost microscopic scale. The distortion is a larger-scale sideways deformation of the tread in plan as it passes through the contact patch. For simplicity, the distortion is often pictured as shown in figure 9, with each element of rubber snaking through a zig-zag pattern (see for example [11]). In practice, the tread of a modern radial tyre is made as stiff as possible in the lateral direction, and as figure 10 shows, the trajectory follows a somewhat smoother curve that has been described as a ‘semi-banana’ [18].
Figure 9
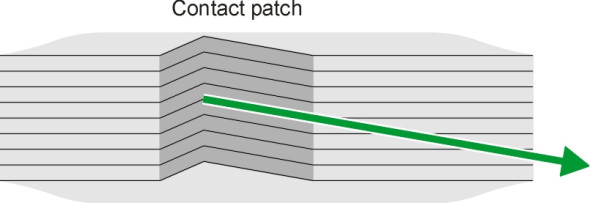
Figure 10
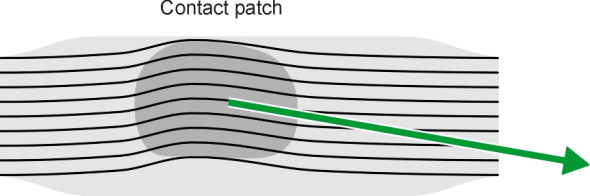
For any given tyre, the size of the slip angle depends on the sideways force. We will denote the sideways force on a tyre by the symbol \(Q_{y}\), in which the subscript \(y\) indicates the force is at right-angles to the direction of motion. Let us fix attention on the outer rear wheel of a car that is travelling round a curve of constant radius. Choose a speed such that the side force on the tyre amounts to 15% of the vertical load carried by that wheel. This is not a very harsh manoeuvre, so typically for a US radial tyre the slip angle will be quite small, about 1\(^\circ\) [14].
If the driver takes the bend faster, the side force must increase, and the tyre slip angle will increase in proportion. Earlier in Section C2015, we tried to explain this relationship mathematically using a simple model. Here we’ll just treat it as an empirical fact. At normal cornering speeds, the relationship between slip angle and cornering force is roughly linear, and the slope of the curve represents the lateral force required to produce a 1\(^\circ\) slip. Technically known as the cornering stiffness, it is a useful parameter that characterises the behaviour of any particular model of tyre [13]. We shall denote it by \(k_C\), thus:
(1)
\[\begin{equation} Q_y \quad = \quad k_{C} \alpha \end{equation}\]If \(\alpha\) is measured in degrees, the constant \(k_C\) must be expressed in newtons per degree. Notice that the normal contact force is not mentioned, as if the tyre could develop this lateral friction regardless of the load it were carrying. This is plainly not the case, not least because the inside rear wheel on a sharp bend can lift almost clear of the road, when it is in no position to provide any grip at all. So the formula can be applied only to situations where the tyre is carrying a load close to its normal rated value.
There is of course a limit to what any tyre can do. The side force peaks when the slip angle is about 20\(^\circ\), and afterwards dips to a lower plateau [4]. But it’s possible to change the stiffness so the peak occurs at a smaller slip angle, which makes the steering more sensitive to the driver’s control movements. Several factors affect cornering stiffness, which together with the ones already mentioned are the subject of keen interest among motoring journalists, whose verdict on a car’s manoeuvrability can make or break its reputation and sales.
- Positive camber: the front wheels of pre-1940 sports cars were often aligned not vertically but leaning slightly outwards, which tends to reduce the cornering stiffness for reasons explained in Section C1405. It may also have reduced the maximum friction itself, because with positive camber, the tyre cross-section can readily lift at the inside edge in such as way as to reduce the area of the contact patch [25]. (This may be why in recent years, the front wheels of F1 grand prix cars have often been set up with negative camber.)
- Tyre construction: radials have higher stiffness than cross-ply tyres because the belt is stiffer laterally and resists distortion [14].
- Aspect ratio: low-profile tyres have roughly double the cornering stiffness of conventional radials, and need a correspondingly smaller slip angle to produce a given side force [14]. They are favoured by drivers who like responsive steering.
- Inflation pressure: cornering force increases with inflation pressure [15]
Finally, regardless of any other consideration, it is vital that the slip angles for the front and rear axles are approximately the same, otherwise the car is likely to mishandle on curves or in a side wind (see Section C0418).
Conclusion
Like all road vehicles, cars are controlled by forces applied through the contact patch of each tyre. There is a maximum force that can be applied through a tyre, and whenever the horizontal force on the tyre exceeds this threshold, the tread begins to skid over the road surface, usually with a loud screech. This is an ominous signal because (a) friction is being wasted (see Section G2016), and (b) the tyre no longer has any preferred direction of motion and therefore cannot guide the car in the direction it is pointing. If both front wheels ‘lock up’ during an emergency stop, the car will continue in a straight line until the driver releases the brake pedal and the wheels start to turn again. If the rear wheels lock, the car will rotate (see Section C0415). Similarly, on a sharp curve if the lateral force on one or more tyres exceeds the threshold, the car will veer off course in a way that most drivers find very difficult to control.
Because rubber is different from other materials, the relationship between the maximum friction force \(F\) and normal contact force \(N\) for a tyre is not precisely linear, and when loads are transferred between wheels during braking and cornering, some grip is lost overall. However, if we ignore the losses, we can still think of the control force on the car as a whole as having a limiting value equal to the coefficient of friction \(\mu\) times the normal contact force, which on a level road is \(Mg\) were \(M\) is the mass of the vehicle. This represents an upper bound or envelope which limits what the driver can do. It also defines the range of forces that the passengers are likely to experience. Compared with travel by rail, sea or air, this is quite a wide range. Since on a good quality road surface in dry weather \(\mu\) is typically around 1.0, the total control force in any direction can approach a value of \(1.0 \times Mg\). Since force = mass \(\times\) acceleration, the acceleration (negative in this case) can reach a value in the region of \(1g\) or 9.81 m/s2. If driven violently, when a car goes round a bend the passengers could experience a sideways acceleration of \(1g\), or to put it another way, the force they will experience as they are thrown sideways against the car interior will usually be the equivalent of their own body weight. The only other place where ordinary people can expect to encounter forces at this level is on a fairground ride.
Loose ends
Hysteresis grip is not affected by a film of oil. Is it affected by ice, and if so, why?