
© Susanna Rosti Rossini
F.2020
Fluid flow
Water is a fluid. Although it looks and feels different, air is a fluid too. Like water, it behaves as if it were composed of slippery particles. When an object passes through it, the particles divide, flow around the sides, and return to fill the void that would otherwise be left behind. A fluid can do this because of its molecular structure. The molecules are not permanently linked, and in fact they continually change position so the fluid body has no fixed shape. Nevertheless, it can exert a powerful force. Sometimes we can feel it on our skin; for example, when walking outdoors, the wind tugs at our clothes and occasionally pushes us off-balance. In calm weather, we create an artificial wind when we move around, a headwind that resists our progress and tends to slow us down. The resistance is negligible at walking pace, but it rises sharply with increasing speed. When travelling on a motorway at 120 km/h, a car’s aerodynamic ‘drag’ accounts for three quarters of the total resistance and hence for most of the fuel consumed [7]. But resistance is not the only issue: air flowing over the roof can apply a vertical force large enough to destabilise a sports car, and when exploited by the aircraft designer, aerodynamic ‘lift’ can support a 450-tonne passenger jet.
Water can support a vehicle too. By virtue of its buoyancy, a merchant ship can float on the water surface, its weight spread over a large area of hull so it can carry a quarter of a million tonnes of cargo inside a relatively thin shell. The hull itself (or least the part that is immersed in the fluid) becomes the ‘contact patch’. Buoyancy is a distinct force, whose value depends only on the amount of water displaced, not on the vehicle’s speed. Fluid resistance and lift, on the other hand, are dynamic forces. They operate only when the vehicle is moving, and they leave a tell-tale signature: a change in the momentum of the fluid particles in the vehicle’s wake. To understand how such forces are delivered, it helps to know what is going on inside the fluid. We’ll start with the internal structure of gases and liquids at the microscopic level, then move on to the pressures and stresses they apply to the vehicle body surface.
Molecular structure
The word ‘gas’ comes from the Greek ‘kaos’. It’s a good name because in a gas, the molecules are always on the move. They don’t stick together, but dart about and frequently collide with one other along the way (figure 1). Imagine a coffee jar standing on the kitchen table. Inside are some coffee grounds, together with a blanket of air containing some aromatic molecules. Were you to look inside, you’d see nothing out of the ordinary, but as the physicist Jennifer Coopersmith explains, the molecules are moving randomly in all directions at speeds of the order of several thousand kilometres per hour [1]. That’s pretty fast, and you’d imagine that if you opened the lid, they would burst out and within a few milliseconds, scatter themselves all over town. At the beginning of the 18th century, that’s how people including Isaac Newton imagined that fluid particles moved, independently like grains of sand. In the spirit of an 18th century scientist, imagine you’re running along the street. How much resistance will you feel? You might start by assuming that particles rain down on a stationary surface at a steady rate per square millimetre. Per unit time, more particles will impact the front of your body than your back, so there will be a net force opposing your motion. You can predict its value using Newton’s laws of motion, because the particles will bounce off your body like rubber balls, robbing you of momentum in the process.
Figure 1
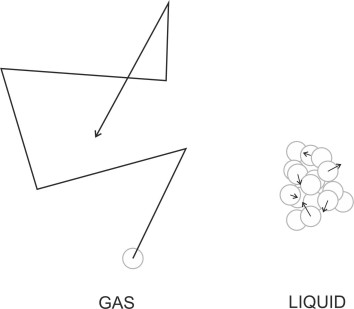
But this is not what happens. Only a tiny proportion of the particles actually reach the surface of your body because they get in each others’ way. In 1859, James Clerk Maxwell calculated that every second, each molecule in the air collides with 8 billion neighbouring molecules [6] following a zig-zag path between collisions so it has no discernible course, no overall direction of movement. So when you run along the street, most of the molecules in your path will be pushed out of the way before you reach them. They’ll be deflected by those in the layer closest to you, acting as a shield within which all the molecules are too busy colliding with each other to collide with you. This is why the air behaves as a smooth and continuous substance that follows a coherent set of streamlines around your body. And why the smell of coffee in a jar takes several seconds to cross a room after you open the lid.
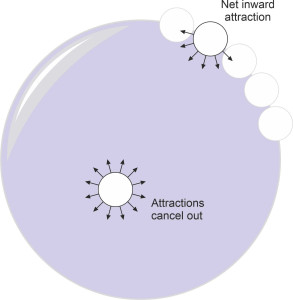
So what about liquids? The molecules in a liquid move around too, and if you pour some into a jar, the liquid will change its shape to fit the container. But unlike a gas, it will run to the bottom and stay there because liquid molecules are electrically attracted to one another and can’t quite get free. They bustle around in close contact, so close in fact that under equilibrium conditions there is little empty space between them. If you squeeze them together they repel strongly, like ball bearings. This is why a liquid can’t easily be compressed: when forced into a container under pressure, water behaves like a solid, and doubling the pressure from 1 atmosphere to 2 atmospheres has little effect, causing the volume to shrink by only 0.03\(\%\) . Water molecules also resist being pulled apart, although the attractive force operates only over a short distance; it is of the same order of magnitude as the size of the molecules themselves, whose diameter is roughly 2.75 angstrom or 0.275 nanometres. It’s also quite weak. Nevertheless, you can see the attraction at work whenever it rains. At the beginning of its journey downwards, a raindrop is roughly spherical in shape. Inside, the molecules cling together – if they didn’t, the raindrop would evaporate before it reached the ground, in fact it would never have formed in the first place. Here, the attractive forces act equally in all directions, while as figure 2 shows, for molecules nearer the surface there is a net attraction that draws them inwards towards the centre, as though under a tightly stretched skin. The phenomenon is called surface tension, although in reality there is no skin and no tension.
Figure 2
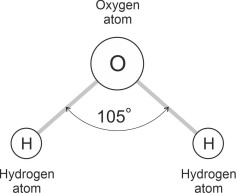
Why do the molecules attract one another? As shown in figure 3, a molecule of water (H2O) is made of three atoms, two of hydrogen (H) and one of oxygen (O). Each atom has a positively charged nucleus surrounded by one or more negatively charged electrons. The hydrogen atoms have one electron each while the oxygen atom has eight. When bound together in a single molecule, the electrons are not uniformly arranged around the periphery: in some places there is a net negative charge and in others a net positive charge where the field associated with the oxygen nucleus dominates.
Figure 3
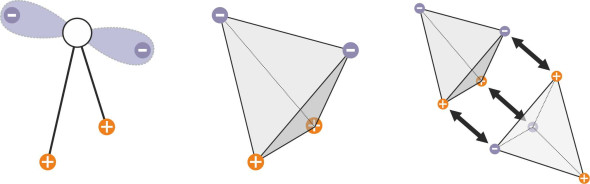
The result is an electrical field with a tetrahedral geometry in which two corners are positively charged and two are negatively charged as shown in figure 4. As you can imagine, the charged corners mean that if they come into contact in a particular way, neighbouring molecules cling together. But they don’t cling for very long, because each is in perpetual motion [4]. The movements are of two different kinds. First, the molecule vibrates about its current position, completing a cycle very roughly every \(10^{-13}\) seconds. Second, it moves bodily at a much slower rate. Around every \(\sim 4 \times 10^{-12 }\) seconds it will either spin around from one orientation to another in response to the movements of its neighbours, or jump for a distance comparable to the average separation between molecules [5]. Since the molecules are jostling together in a crowd, they cannot easily break free, and each slips between its neighbours one step at a time.
Figure 4
With all this movement going on, you might suppose water to have a completely random structure, but this isn’t quite the case. From time to time some of the molecules will cling together briefly in a formation that hints at an underlying hexagonal geometry. If you cool the water below 0\(^{\circ}\) C, the geometry becomes locked into place as the molecules form ice crystals. The attractive forces have another consequence too. The molecules will stick to any hard surface with which they come into contact, so that when air or water flows around a moving body, a thin sheet of particles clings to the surface and slows down the neighbouring layers. The result is called a boundary layer, and it will feature prominently in Section F1917.
Pressure
We are taught at school that a fluid will exert pressure on any body with which it comes into contact (by ‘pressure’ we mean normal pressure acting at right-angles to the body surface). Where does this pressure come from? Picture the air inside an otherwise empty container at room temperature. The constituent molecules (mostly oxygen and nitrogen) bounce off the walls at a rate of around a billion per square centimetre per second [1]. The repeated impacts tend to push the walls outwards, and since the impacts are tiny and they occur at very high frequency, the surface ‘feels’ a steady pressure. Furthermore, a gas is compressible so if we squeeze it into a smaller volume at the same temperature, each molecule will travel a smaller distance before reaching the wall, and every second there will be more impacts and the pressure will rise accordingly. Although it’s beyond our scope here, the well-known ‘gas laws’ relating pressure, temperature and volume can all be deduced from statistical analysis of these impacts under various conditions. So how does this affect vehicles moving about in the open air? Within the earth’s atmosphere there is a measurable difference in air pressure between sea level and the highest mountain peaks because the air molecules are influenced by gravity and collectively, they behave like a stack of horizontal layers piled up above the earth’s surface. Although they are very light in weight, the upper layers squeeze the ones below so that both the pressure and density rise approaching the earth’s surface. Conversely, the pressure and density fall with increasing height. The effect is noticeable for a passenger jet that may well cruise at 10 000 metres where the conditions are very different from those on the ground.
In the case of a liquid such as seawater, there are two main differences. First, seawater is almost incompressible and doesn’t like to be pulled apart so its density \(\rho\) is the same throughout the whole liquid mass. Unlike the air, it can’t diffuse freely to create a rarefied atmosphere, but rather, the particles stick together and form a well-defined liquid surface. Second, it is much denser than a gas and the pressure rises very quickly below this surface. Hence, when a ship lies at anchor in a calm sea, the pressure distribution on the hull increases with depth at a steady rate. You can work out the relationship between pressure and depth by picturing the water as divided into vertical columns each of cross-section one square metre say. The water at depth h is supporting the weight of the column above it: the volume of the column is h\(\times\) 1 = h cubic metres, its weight is \(\rho\)h kg, and the downward force it exerts on the water below is \(\rho\)gh newtons where \(\rho\) is the mass density of the water in kg/m3 and \(g\) the acceleration due to gravity. So the pressure is \(\rho g h\) N/m2. It doesn’t just act downwards. It acts sideways as well – indeed equally in all directions. Like me you may have been puzzled when you were told this at school. We were taught that if you apply a force to something and it doesn’t move, it will push back in the opposite direction: action and reaction are equal and opposite. If the weight of the water only acts downwards, where does the sideways pressure come from?
Figure 5
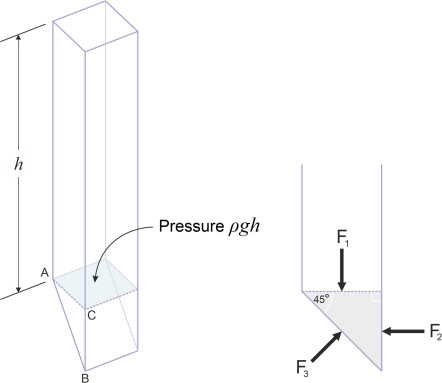
A simple explanation runs as follows. The column of water is shown in figure 5, with a wedge-shaped chunk of fluid tacked on the bottom whose cross-section has the shape of a 45-degree triangle ABC. Suppose the water above presses down on the chunk with force \(F_{1}\). It is balanced by a force \(F_{3}\) pressing upwards on the inclined plane underneath. But this force must be at right-angles to the inclined plane, because any other angle implies a shear component, and a fluid can’t resist shear forces at least not when stationary (we’ll say more about this in a moment). We are interested to learn whether or not there might be a lateral force \(F_{2}\) acting on the right-hand face. If there is, it must be aligned horizontally as shown. Now let’s resolve forces parallel to the inclined plane. There is a component of \(F_{1}\) acting downwards and to the right along the inclined plane and its value is equal to \(F_{1} \cos45^{\circ}\). It must be balanced by an equal force in the opposite direction. The only force available is \(F_{2}\), which again acts at \(45^{\circ}\) to the angle of the inclined plane. So
(1)
\[\begin{equation} F_{1} \cos 45^\circ \quad = \quad F_{2} \cos 45^\circ \end{equation}\]from which we see that \(F_{2} = F_{1}\), and since the areas on which the two forces act are equal, the pressures must be the same.
Shear stress
Now we turn to a different but related phenomenon, shear stress. It’s like normal pressure except that its acts in a different direction – tangentially along the surface to which it is applied, as happens when you slide your hand over a table top. The idea of shear stress occurring in a fluid seems odd at first. According to one definition, a fluid is a substance that cannot sustain a shear stress, at least not when at rest. What this means is shown in figure 6. Two bars are connected by a steel pin. The first bar could be the drawbar of a tractor, and the second, the attachment to a trailer, and the pin, which passes vertically through a hole in each bar, has to transfer the load between the two. The tractor is trying to pull the trailer from left to right. When it starts to pull, the pin undergoes a shearing action and as long as it doesn’t break, the trailer will follow. Now take out the pin and pour some water in its place (you’ll need to plug the bottom hole so the water doesn’t run out). When the tractor starts to pull, the water won’t stop the bars sliding apart: it has no shear resistance.
Figure 6
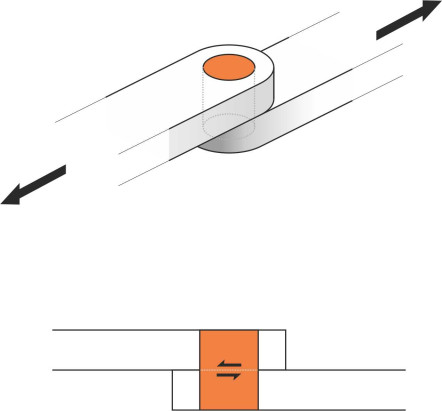
However, this is not the whole story. In fact, a fluid can transmit a shear stress, but only when different layers within the fluid body are shearing across one another at a perceptible rate – there has to be continuous distortion and therefore continuous movement. Under these conditions, a shear stress arises because all fluids – including gases – are viscous. The stress acts not only among layers within the fluid mass, but also between the fluid and any rigid boundary over which it is moving, an effect not very different from friction. When a swan lands on water, it lowers its feet so they scrape along the surface and the friction helps to slow it down.
Figure 7
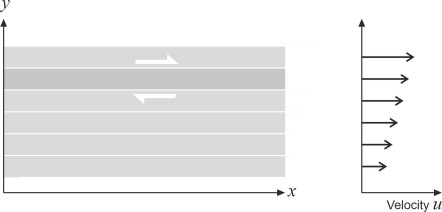
The friction is small but it increases with the rate of distortion. Imagine a smoothly flowing stream of fluid with consecutive layers each moving slightly faster than the one below. The speed \(u\) of any given layer is proportional to its vertical distance \(y\) above datum, measured at right-angles to the direction of flow as shown in figure 7. The direction of the shear stress \(\tau\) acting on one of the layers is indicated by red arrows. Its value is proportional to the shear rate \(du/dy\) and is given by the formula
(2)
\[\begin{equation} \tau \quad = \quad \mu \frac{du}{dy} \end{equation}\]The constant \(\mu\) is the coefficient of viscosity or dynamic viscosity. Its value is about \(1.79 \times 10^{-5}\) N s m\(^{-2}\) for air at sea level, and about \(108 \times 10^{-5}\) N s m\(^{-2}\) for seawater at \(20^{\circ}\)C. Many prefer to use the kinematic viscosity\(\upsilon\) instead:
(3)
\[\begin{equation} \upsilon \quad = \quad \frac{\mu}{\rho} \end{equation}\]where \(\rho\) is the mass density of the fluid. The value of the kinematic viscosity for air at sea level is about \(1.46 \times 10^{-5}\) m2 s\(^{-1}\), and for seawater at \(20^{\circ}\)C it is about \(0.105 \times 10^{-5}\) m2 s\(^{-1}\).
So what causes a fluid to resist sliding? In a gas, the molecules are continually moving between adjacent layers. Referring to figure 7, molecules escape from the faster-moving layers at the top and transfer some of their momentum to molecules in the slower-moving layers below, speeding them up in the process. Conversely, molecules in the slow-moving layers diffuse upwards and slow down the faster ones. Hence molecular diffusion tends to smooth out the velocity difference. The effect is small, but it makes all gases slightly viscous. In a liquid, the mechanism is different. Provided the flow is smooth rather than turbulent, there is much less diffusion of molecules across the layers than would normally occur in a gas, and it is the electrostatic attraction between neighbouring molecules that accounts for most of the viscosity [3]. If the flow were turbulent, there would be a good deal of mixing as well, so the viscosity effectively would increase.
Shear stress makes the analysis of fluid motion more difficult than analysing the motion of mechanical objects like a pendulum or a clockwork motor. So if you want to forecast the flow pattern of air or water round a moving vehicle it’s a good idea to ignore the shear stress – at least to begin with – and assume that the viscosity is zero. An inviscid fluid is an exotic material. If you put it in a sealed container such as a plastic bag it will resist squeezing, but outside it becomes too slippery to hold - you can’t grasp it and turn it in yours hands like a doorknob because the particles don’t respond to frictional shear forces. Unless they are already rotating, no interaction with your hands or indeed with anything else will work. Nor will an inviscid fluid exert a net force on a moving vehicle, so after working out the flow pattern one has to modify the results to allow for the additional forces that arise within the boundary layer close to the body surface, and also within the vehicle wake.
Fluid mechanics
This part of the web site contains thirteen Sections that deal with the interaction between moving vehicles and the air or water that surrounds them. They are bundled together in this way because the same principles apply to all kinds of vehicle: they belong to the wider discipline of fluid mechanics, one of the most demanding topics in engineering science. What follows is intended to support the mainstream material, and you may find it useful to dip into it rather than treating it as a crash course.
Acknowledgement
Photo on opening page by Susanna Rosti Rossini