G.2016
The laws of friction
What do you do when you wake up in the morning? Maybe you throw off the bedclothes and put on your dressing gown. Then after visiting the bathroom, slide down the banisters ready to begin a new day. All these activities involve friction, the ability of materials to resist sliding over one another when their surfaces are pressed together. Without it life would be impossible: the bedclothes wouldn’t stay on the bed long enough for you to sleep under them, and since you couldn’t tie knots, the cord on your dressing gown would be useless (and the fabric itself would have disintegrated long ago). You couldn’t walk to the bathroom, although you might try skating along the carpet. Finally, the bathroom would be flooded because the taps wouldn’t stay screwed to the pipework.
Because they are so important, we are taught ‘the laws of friction’ in school. They were first codified around 500 years ago and refined during the 18th century. They are not fundamental in the same sense as Newton’s laws of motion, but rather, approximate rules that emerge from some fascinating and complex properties of solid materials at the molecular level. These properties are determined by events within a surface layer that may be only a few molecules thick. It’s not just a matter of smoothness, but also chemistry, because almost all materials form a surface layer whose composition is different from the underlying mass. This applies to glass, plastics, and even diamond. When exposed to the atmosphere, most metals develop an oxidised coating within minutes [4].
What the laws say
The laws of friction apply to surfaces that are not lubricated in any way. Imagine a glass jar resting on the horizontal surface of a wooden table. Its base is smooth, flat and square, measuring 100 mm by 100 mm. The jar will press vertically down on the table by virtue of its own weight, so it is exerting a force at right-angles to the surface that is known as the ‘normal contact force’, denoted by \(N\) (figure 1). The friction force acts parallel to the surface. If we try to push the jar sideways it will resist, and the heavier the jar, the more difficult it is to move. Under these conditions, smooth, rigid materials like timber, glass and steel obey three well-known rules.
- The frictional resistance is proportional to the force exerted by the object at right angles to the surface. More precisely, the maximum resistance \(F\) is given by the normal contact force \(N\) multiplied by the (static) coefficient of friction \(\mu\), thus:
(1)
\[\begin{equation} F \quad = \quad \mu N \end{equation}\]
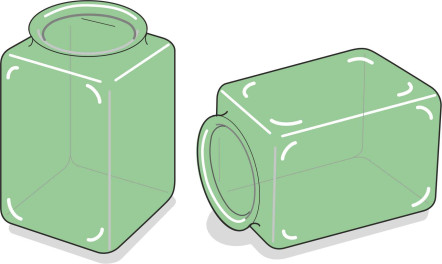
The coefficient \(\mu\) has a fixed value for any particular combination of two materials in contact. In the example mentioned earlier, since the normal contact force derives solely from the jar’s weight its value is just \(Mg\) newtons, where \(M\) is the mass of the jar and \(g\) the acceleration due to gravity. But it could easily be altered by tilting the table, or filling the jar with water. - The frictional resistance is independent of the area of contact, so the normal contact force can be concentrated over a small area or spread out over a large one – it makes no difference. If our glass jar had flat sides, even if they were much larger than the base, say 200 mm by 100 mm, we could turn the jar on its side and the frictional resistance would be unchanged (figure 2).
- Once the object starts to slide, the resistance usually falls to a lower value \(F_s\) say. This sliding friction or kinetic friction is again proportional to \(N\), so we can write
(2)
\[\begin{equation} F_s \quad = \quad \mu_{s}N \end{equation}\]
where the coefficient of sliding friction \(\mu_s\) is usually less than the coefficient of static friction \(\mu\). Its value is roughly constant regardless of the speed of motion.
Figure 1
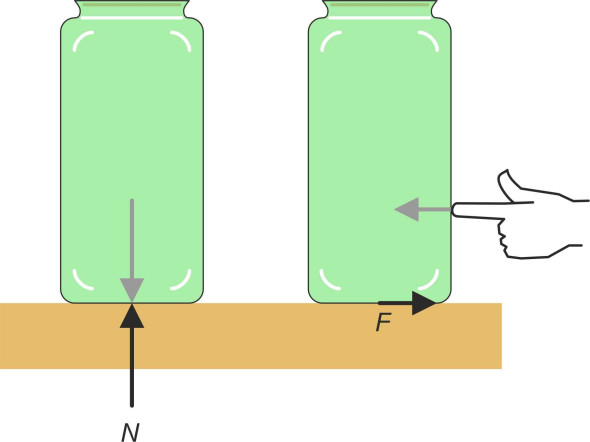
Figure 2
Where do they come from?
The first two rules were established by the 17th century French architect and science philosopher Guilluame Amontons [1]. If you think about them for a moment, these rules are quite remarkable. It is not immediately obvious why doubling the load on a glass jar should double the friction, nor how the area of contact can be increased or decreased without affecting the outcome. But scientists soon devised an explanation based on the idea that friction arose from tiny projections on each surface. Indeed, examination through a microscope will confirm that what might appear to be a smoothly polished surface is far from smooth at high levels of magnification. The projections were thought to interlock, like two sheets of sandpaper grating together.
A tentative model
Let us pursue this idea for a moment – the results will be useful later on, not least because they demonstrate that resistance can occur even when the surfaces slide over one another without any shear forces at all, as if they were perfectly lubricated. For simplicity, we’ll assume a model in which the two surfaces are ridged, with regularly spaced teeth that interlock across the whole area of contact. This model was originally posited by the French scientist Coulomb during the late eighteenth century [2] and was also investigated by the mathematician Euler [7]. Figure 3 shows the arrangement in cross-section. Each tooth has two straight sides, both at angle \(\theta\) to the plane of contact. The two surfaces are squeezed together with a normal contact force \(N\).
Figure 3
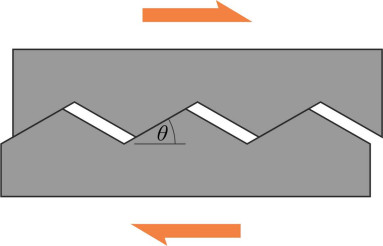
For the upper surface to slide over the lower one, it must move a short distance upward and to the right at angle \(\theta{}\) until the crests of the teeth pass over the crests of the teeth in the lower surface and engage in the next set of valleys. We stipulate that there is no friction between the two surfaces. What is the largest horizontal force that the block can sustain before moving?
Figure 4
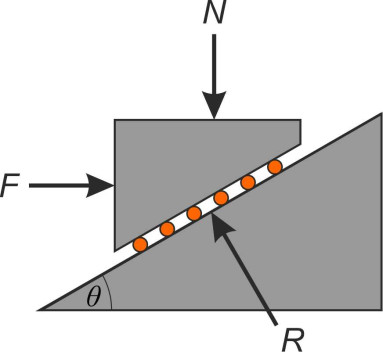
The set-up can be represented by a trolley moving up a sloping surface on frictionless rollers as shown in figure 4. Resolving vertically and then horizontally, we get
(3)
\[\begin{equation} N \quad = \quad R \cos \theta \end{equation}\](4)
\[\begin{equation} F \quad = \quad R \sin \theta \end{equation}\]from which it is clear that
(5)
\[\begin{equation} F \quad = \quad N \tan \theta \end{equation}\]In other words, the lateral resistance to motion is proportional to the normal contact force. The term \(\tan \theta\) plays a similar role to the coefficient of friction \(\mu\) in equation 1, being a constant that depends only on the characteristics of the surfaces concerned. So our tentative model predicts the first ‘law’ of friction rather well. Unfortunately, it’s wrong.
Asperities and molecular forces
In real life, surfaces are more complicated, and it was not until well into the 20th century that the truth was finally uncovered, and set out in a historic publication that has recently been revived in a facsimile edition [3]. Friction is the action of electrical forces between molecules on either surface. These forces have an extremely small range, and for them to come into play the two surfaces have to be in very close contact. Let’s assume for the moment that both materials are rigid, not soft and flexible like rubber. Each surface is covered with peaks or ‘asperities’ of varying height, so that when the two are brought together, they touch only in a few places - elsewhere the gap is too large for the molecular forces to bridge. The area over which the surfaces are actually in contact is a tiny proportion of the apparent contact area. Because the peaks are so small, it takes only a gentle force pressing the surfaces together to crush them, and the frictional characteristics are determined entirely by the behaviour of these minute areas under extreme stress conditions.
Friction for different materials
Therefore in order to explain the relationship between friction and normal contact force, we must focus on what happens within these areas. We’ll break the process down into two stages: first we apply only a normal contact force, then we add a shear force to make the surfaces slide over one another.
Metals
When two metal specimens are pressed against one another, the peaks don’t break, but rather they yield, flowing like molten lava as soon as the stress passes a certain threshold. This yield stress has a fixed value, so at every point where the surfaces are in contact, the true normal stress is more-or-less the same. What happens if you press harder? The yield stress can’t change, so the areas of contact expand in proportion to the normal contact force (figure 5).
Figure 5
Now for the shear force. If we try to slide the two surfaces over one another, we find that the high spots are continually pressure-welded together, then torn apart in a process described as ‘slip-stick’ [6]. It is the force needed to tear them apart that manifests itself as friction, and its total value increases linearly with true contact area (figure 6) - and we know that the true contact area is in turn proportional to the normal contact force. Although we have skated over the details a little, this explains why friction is proportional to normal contact force.
Figure 6
Many other materials behave in roughly the same way, except that the relationship between normal contact force and friction force is not exactly linear, and therefore friction is not entirely independent of area. The value of the coefficient of friction for any given combination of materials cannot be predicted in advance and must be determined by experiment. Observed values range from 0.04 for the sliding friction of Teflon on Teflon, to 4 for rubber on steel [5].
Rubber tyres
Being flexible, rubber will mould itself around asperities on the surface of a harder material. Hence the true contact area is much greater than is the case for metals, and there are no stress concentrations that in a metal would lead to plastic flow. Nevertheless, the true contact area, and hence frictional resistance, increases with normal contact force \(N\) because as the normal stress increases, the rubber surface works its way more deeply into the crannies between the asperities. But the relationship is not linear: the friction doesn’t increase exactly in proportion with \(N\), a property that has interesting consequences for car tyres (see Section C1717).
And there is another difference. Rubber is one of a special class of materials for which the resistance to sliding is actually made up of two distinct components: conventional friction as described earlier, which we call the adhesion component, and a second component hysteresis which arises in a completely different way (see Section C1717). The hysteresis component accounts for less than half the total, but unlike adhesion it keeps working even when the surface is wet, a property for which travellers have reason to be grateful.