C.0816
Stopping
Imagine you are waiting to cross the road. You know that if you step out in front of a moving vehicle you are likely to get hurt because it won’t stop immediately. A moving car has energy simply because it is moving, and it can only stop if this kinetic energy is transferred into some other form. The transfer process takes time, and since the value of the kinetic energy is equal to half the vehicle mass times the square of its speed, then other things being equal, the more heavily loaded the vehicle and the faster it is moving the longer it takes. For most wheeled vehicles with conventional brakes, the kinetic energy is turned into heat by pressing brake pads against disks or drums that are fixed to the wheels. The heat generated at the interface flows mainly into the disk, and as the disk cools it is given up to the gas molecules in the surrounding air. The vehicle stops and the molecules move instead.
The vehicle, the wheel, and the road
So how much kinetic energy does a moving car contain? For a family saloon weighing 1.5 tonnes and travelling at a motorway cruising speed of 120 km/h, the answer is a little over 800 kilojoules (kJ). In heat terms, this is the amount needed to boil a large kettle of water. It may not sound very much, but what matters is the rate at which it can be dissipated. Assuming a constant rate of deceleration of 0.5\(g\) while braking to a standstill, the whole of the 800 kJ must be transferred in just under 7 seconds, so during an emergency stop, our passenger car brakes would generate heat at a rate of about 120 kW, equivalent to forty 3 kW electric fires carried inside the wheel arches.
But in practice, an emergency stop is not the biggest challenge for the engineer, because the heat that it generates can be stored temporarily within the brake drum or disc to be radiated into the surrounding atmosphere later. A bigger challenge comes during a long downhill descent, when the driver may need to apply brake pressure continuously to hold the car at a steady speed. Here, it is potential energy that must be converted into heat. In the case of a 1.5 tonne car travelling at a steady speed of 80 km/h on a downhill grade of 1 in 10, the energy dissipation rate is equivalent to 33 kW, and it must be sustained continuously until the car reaches the bottom. This may take several minutes, and although the brakes receive help from air resistance and other sources, direct cooling to the atmosphere is essential to stop the components from melting [8].
Wheel slip
However powerful they might be, brakes will not stop a car if the tyres don’t grip the road. We have already encountered the contact patch, where friction develops between the tyre tread and the road surface (see Section C1717). According to the conventional model of surface friction, when two materials are placed together in shear, the frictional resistance is greatest when there is no relative motion between the two. If one surface slides over the other, the friction is immediately reduced. However, as a visco-elastic material, rubber behaves differently, and up to a certain point, friction actually increases with relative motion. It has even been questioned whether viscoelastic materials have any static friction at all [16].
So let’s imagine a bus cruising along an urban motorway. Something appears in the distance ahead, and the driver presses the brake pedal, gently at first then progressively harder as he realises that the road is blocked. Let’s concentrate on one of the front wheels and watch what happens to it as the braking effort increases. As passengers we are hoping to see the rubber firmly planted on the road surface, generating a high level of ‘static friction’ rather than sliding friction of the kind that occurs during a skid. However, where pneumatic tyres are concerned, the friction is not actually static. The reason is that the rubber tread develops its grip by creeping over the road surface, especially when the surface is wet. By creeping, we don’t mean creeping at the speed, say, of a caterpillar. The rate of creep can be quite fast. Hence under braking, the wheel rotates at a speed appreciably less than that of a freely rolling wheel [1]. The difference is called the slip ratio S, usually expressed in percentage form via the equation:
(1)
\[\begin{equation} S\quad = \quad \frac{\Omega_{free} \; - \; \Omega_{actual}}{\Omega_{free}} \; \times \; 100\% \end{equation}\]where \(\Omega_{free}\) is the angular velocity of a freely rolling wheel without any braking action, and \(\Omega_{actual}\) is the angular velocity of the braked wheel [2]; there are several variants of this definition that amount to the same thing as can be seen for example in [6] and [12]. When no brakes are applied, the angular velocity equals that for a freely rolling wheel and \(S\) is zero. When the wheel locks, the tread is stationary relative to the car and \(\Omega_{actual}\) is zero, so that \(S =\)100%. The braking force peaks when the slip ratio is about 20% [14]. Hence if the car is travelling at 100 km/hour, at peak braking effort the tyre tread is ‘creeping’ along the road surface at 20 km/h.
The challenge for the driver is that with light braking, the bus may not stop in time. But if the driver brakes too hard, the wheel will skid, the grip will diminish, steering may be lost, and the bus will take longer to stop than it would otherwise do (figure 1). Somewhere between lies an optimum brake pressure that uses all the available grip between the tyre and the road. In fact, it is quite rare for a driver to get the brake pressure right, or even approximately right. Most of us who drive private cars don’t stamp on the pedal hard enough, possibly because we are afraid of losing control.
Figure 1
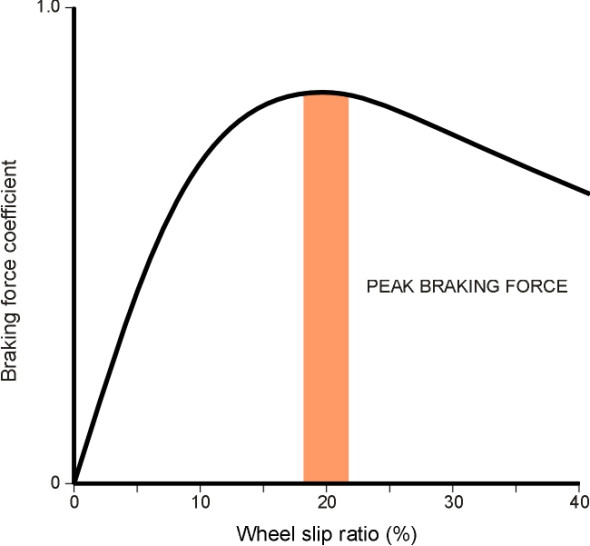
Braking force coefficient
Assuming you could press with exactly the right force on the brake pedal, what is the maximum friction could you expect to obtain between tyre and road surface? Because tyres perform differently depending what they are being asked to do, the friction coefficient under braking is given a distinctive name: the braking force coefficient, or BFC for short. It refers to braking in a straight line. Values of the BFC vary greatly with the material of the road surface, the condition of the tyres, and the weather, and some illustrative values are set out in Table 1 of Section C1603. On a good quality road surface in dry weather, we might expect a value of 1.0, and in wet weather about 0.5.
In an ideal world, these figures could be interpreted not only as friction coefficients, but also as rates of deceleration that could be used to forecast stopping distances. For example, a BFC value of 1.0 suggests that the driver can achieve a \(1g\) stop, i.e, a deceleration of 9.81 m/s2. Similarly, a BFC of 0.5 suggest a \(0.5g\) stop, or a deceleration of \(0.5 \times 9.81 = 4.91\) m/s2. You can see why if you compare Newton’s Second Law (force = mass \(\times\) acceleration) with Amonton’s rule (friction force = normal contact force \(mg \; \times\) coefficient of friction; see Section G2016). Unfortunately, one can’t rely on the BFC figures we have quoted because several other factors come into play depending on how the vehicle is being driven:
- BFC falls with increasing speed, so the faster you are moving, the less effective the braking process.
- The portion of the BFC that is available for decelerating the vehicle diminishes on a downhill slope. This is because a component of the vehicle’s body weight acts in the direction of motion, and any such component has to be balanced by a steady braking force just to maintain a steady speed.
- With a conventional braking system, the division of braking effort among the four wheels is fixed according to the characteristics built into the actuation system. But as indicated in Section C2009, braking temporarily redistributes the load between front and rear axles [9] so under most circumstances one or other axle will reach peak braking force and lock while the other is not fully utilised.
This last point means that the braking system for the vehicle as a whole must necessarily fall short of its full potential unless a way can be found to re-balance the braking effort from moment to moment in line with the varying loads on each wheel. This is such an important limitation that we’ll deal with it separately later. But even if it can be overcome, since grip doesn’t increase linearly with normal contact force [13], any extra grip on the more heavily loaded wheels cannot quite make up for the grip lost at the more lightly loaded ones.
Stopping distances
The occasions when a driver has to brake suddenly may be few and far between, but when they arise, the distance required to stop can make the difference between a near-miss and a crash. For the purposes of illustration, therefore, let’s assume that there is a BFC value that describes the braking performance of the vehicle as a whole and hence can be interpreted directly as a deceleration rate which we’ll write as a constant \(b\) times the acceleration \(g\) due to gravity as before. Can we write down a formula for the distance that the vehicle needs to stop in terms of \(b\)?
This distance breaks down naturally into four parts [5]. First, there is the distance travelled between the moment a driver perceives a hazard and the decision to apply the brakes. If the driver is alert (for example, wide awake and not using a mobile phone) this should take less than a second. Call the value \(t_{reaction}\). If the car’s speed is \(v\) it will have travelled a distance \(vt_{reaction}\) before the braking sequence actually begins. Once the decision is made, it takes a further fraction of a second (which we shall denote by \(t_{initiation}\)) for the driver to hit the brake pedal and press it down, together with a few milliseconds before the signal arrives at the brake pads, they engage with the brake disk, the wheel, tyre and wheel bearings take up their various tiny compliances and the tyre tread begins to bite into the road surface. Then there follows a brief period during which the braking effort builds up to a maximum, which might be termed the ‘acceleration rise time’ \(t_{rise}\), but to keep things simple we ’ll ignore this term. Finally, assuming the retarding force on the vehicle is constant throughout the actual period of braking, the braking process will occupy a distance \(v^{2}/2bg\), as you can work out yourself from the well-known constant acceleration formula. Hence neglecting the acceleration rise time, the total distance required to stop is given by
(2)
\[\begin{equation} s\quad = \quad v \left( t_{reaction} \; + \; t_{initiation} \right) \; + \; \frac{v^2}{2bg} \end{equation}\]If you look at it as a power series in \(v\), this formula contains two terms, the first linear, in which distance rises in proportion to speed, but the second term, which dominates in practice, rises as the square of speed. This is reflected in the UK Highway Code (see the web site [25] given at the end of this section), which describes the two terms as ‘thinking distance’ and ‘braking distance’, and sets out values of each for a car travelling at various speeds between 20 mph (32 km/h) and 70 mph (113 km/h). One can work backwards from the contents to deduce that the thinking time is somewhat less than a second, and the deceleration rate about \(0.67g\).
Braking systems
Braking systems work by converting one kind of energy (kinetic energy) into another, usually heat. Pumping heat into the atmosphere is wasteful of course, and over the years, engineers have sought alternative forms of storage so the energy can be recovered for later use: electrical charge stored in a capacitor, for example, or mechanical energy stored in a flywheel or a compressed gas container. Regenerative braking systems are now well established for trams and buses, but they are bulky, heavy and expensive, and although progress has been made with the KERS (Kinetic Energy Recovery System) concept for Formula 1 motor racing, for the time being most of us will have to make do with conventional friction brakes.
Drum brakes
Almost from the beginning, cars were equipped with drum brakes, at first on the rear axle only, and later on all four wheels. The drums are now made from cast iron, or occasionally more exotic compound materials [18]. Each drum contains two brake shoes pressing outwards against the inner cylindrical surface. The brake shoes are lined with a heat resistant material made from synthetic fibres bonded with resin. Prolonged pressure such as might occur while braking on a long descent can soften the resin so that a molten film smears across the friction surfaces. This degrades performance, a characteristic known as brake ‘fade’, but if allowed to cool, the system will quickly recover [3]. The phenomenon was well known to early racing car constructors because it forced the drivers to slow down during endurance events, and it also caused difficulties for lorry drivers and car drivers in hilly country. But the problem was gradually resolved with the emergence of disk brakes during the 1950s.
Figure 2
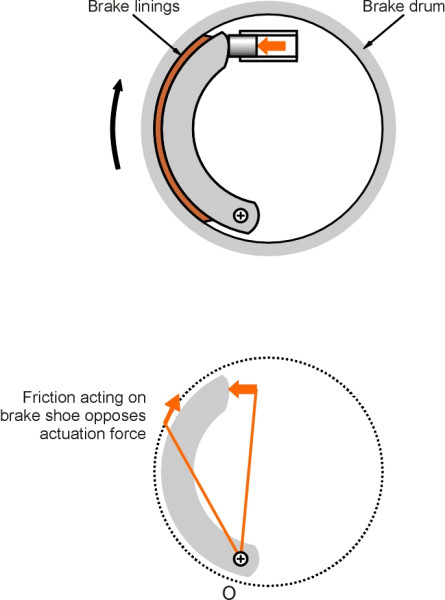
Figure 3
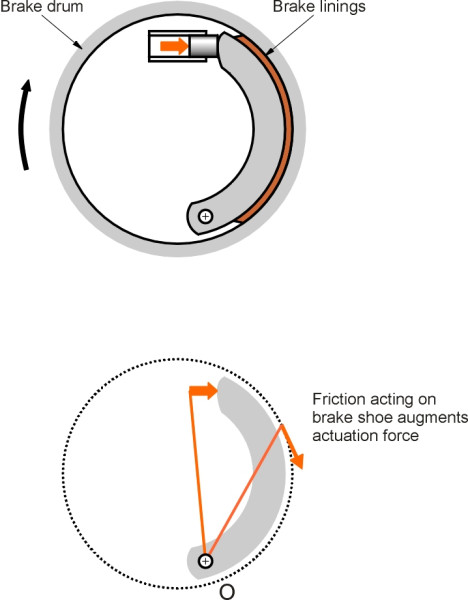
Although disk brakes are now fitted to most private cars, drum brakes are still preferred for heavy vehicles. In principle, a brake shoe can be mounted inside the drum in one of two ways, ‘trailing’ (figure 2), or ‘leading’ (figure 3). A leading shoe provides a degree of self-servo action, because once applied, the friction force itself tends to rotate the shoe about its hinge, effectively increasing the pressure of the shoe on the drum by a factor of about three compared to a trailing shoe [19]. Various combinations of leading and trailing shoe are possible, but it is always useful to have at least one trailing shoe on each rear wheel because leading shoes don’t work very well in reverse.
Hydraulic actuation
Even with self-servo action, considerable force is needed to make friction brakes work. Early drum brakes were operated via a system of levers and cables which magnified the force exerted by the driver’s foot pressing on the brake pedal, but for passenger cars at least, they have largely been superseded by hydraulic actuation. The principle behind hydraulic brake actuation is very simple. There is a continuous sealed pipeline between the driver’s brake pedal and each brake drum. Most of it is rigid tube, with the final connection to the brake drum made via a flexible hose. The brake pedal engages with a piston in a master cylinder. The master cylinder feeds hydraulic fluid under pressure via the four pipelines, each to a slave cylinder inside one of the brake drums. Each slave cylinder in turn forces the tip of one or both brake shoes outwards against the drum wall to slow it down. The cross-sectional area of each slave cylinder is much larger than the cross-sectional area of the master cylinder, and the input force applied by the driver to the brake pedal is multiplied accordingly.
A hydraulic system confers many advantages over a mechanical linkage. It saves weight, it doesn’t need lubricating, there is almost no frictional resistance between moving parts, it automatically equalises the actuation force delivered to each of the wheels, and the flexible hose can easily be routed around obstacles in the crowded space immediately behind the wheel dish where it takes up large suspension movements without accidentally jamming on the brakes. But all this comes at a price, which early developers of hydraulic systems soon discovered. In order to transfer high loads through a narrow tube, the fluid must be virtually incompressible, otherwise the driver can press the brake pedal to the floor without transmitting much force to the brake shoe or disc pad. That means there must be no entrained gases of any kind, which would make the system ‘spongy’ (when you push one end of a column of fluid that contains bubbles, the bubbles compress and the column shrinks). Furthermore, a disc brake pad gets very hot – up to 550\(^\circ\)C – so the fluid must be specially formulated with a high boiling point [8]. And of course, high-quality seals are needed to prevent leakage and to prevent air bubbles from becoming entrained in the liquid.
Disc brakes
By comparison with modern disc brakes, drum brakes are bulky, heavy, and difficult to keep cool. The disc brake was originally developed for aircraft, and successfully transferred to the motor industry after a string of wins by Jaguar at Le Mans in the mid-1950s [20]. The disc itself is lighter and more compact than a drum, and it dissipates heat more easily because the contact surfaces are exposed to the atmosphere (figure 4). Hence a disc brake is less prone to fade.
Figure 4
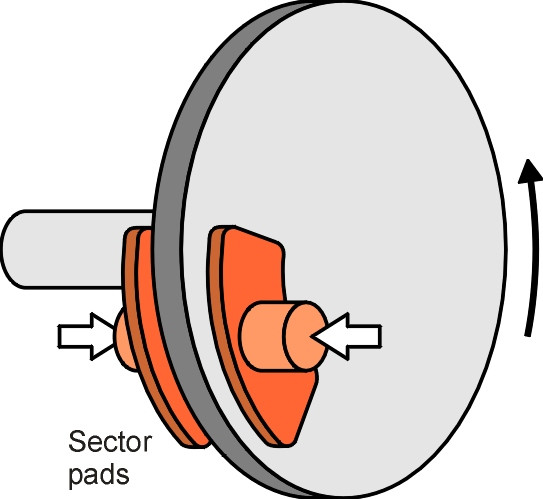
Compactness is a vital factor in suspension design, because with front wheel drive and independent suspension there is acute competition for space within the front wheel arch of a modern vehicle, especially a passenger saloon (see Section C1405). This can only be done by ‘dishing’ the wheel as shown in figure 5. Consequently the disc on a modern car is not actually flat, but shaped like a top hat so the inner portion can be bolted directly to the inside of the wheel, with the friction surface positioned more-or-less on the wheel centreline.
Figure 5
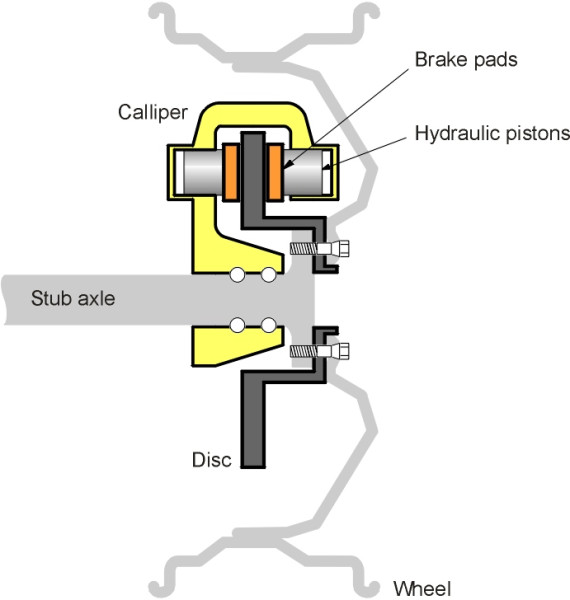
A disc brake does not readily lend itself to self-servo action, but on the other hand, without self-servo, the disc brake jams less easily than a drum brake. In modern vehicles the additional pressure of the brake pads on the discs is supplied by servo assistance – often through vacuum generated in the engine intake manifold, which is connected to a piston that pressurises the hydraulic fluid. If the car has a diesel engine, there is no intake manifold and the fluid needs a separate hydraulic pump.
As shown in figure 4, modern brake pads have what is called a ‘sector’ profile that can be slid into place without dismantling the calliper. There are two pads mounted within a calliper unit so they can grip opposite sides of the disc in the same way that old fashioned bicycle callipers gripped the wheel rim. Various ‘fixed’ and ‘floating’ combinations are possible, of which a detailed account is given in [21].
Disc brake materials
Because of the extreme demands made on them, the two friction surfaces in a disc brake system must be well matched [8]. This doesn’t mean they are made of the same material, because their needs are different. The discs must be structurally rigid and conduct heat well, with high wear resistance. They are usually made of cast iron, although more sophisticated composites are used in high performance cars because they are lighter (and vastly more expensive). The pads, on the other hand, must have low thermal conductivity so that they do not transmit heat to the brake fluid. And since they can easily be replaced, they are designed to wear more quickly than the discs, adapting to surface irregularities to provide good contact over the whole of their working area. They are usually made from particles and fillers bonded together in a phenolic resin matrix with reinforcing fibres. Originally, asbestos fibres were preferred, but pressure to switch to asbestos-free materials has led to alternatives such as Kevlar, glass fibre, steel fibre, aluminium wool, mineral wool, aramid fibre, and carbon fibre [22].
Just as with drum brakes, the pad must be pressed onto the disc with considerable force, in fact more so because there is no self-servo action. Some illustrative figures for brake pad pressures are given in [22]. The maximum operating pressure specified for one particular disc pad is over 5 MN/m2, the equivalent of about 50 atmospheres.
Control
There is more to a braking system than the disks and pads. Performance depends partly on how the hydraulic circuits are linked together. In particular, the braking forces need to be divided between the front and rear axles in a sensible way, and this is more difficult than it might seem. We’ll start by working out the performance that is theoretically possible and use it as a yardstick against which to measure different configurations. Let’s denote the total braking force by \(Q\) (measured in newtons), the coefficient of friction of the tyre-road combination by \(\mu\), and the deceleration by \(bg\). The number \(b\) is dimensionless; we will use it as before to quantify deceleration in multiples of \(g\), where \(g\) = 9.81 m/s2, the acceleration due to gravity. When \(b\) = 0 the car doesn’t slow down at all but continues to move at constant speed. When \(b\) = 1 the vehicle is decelerating at 1\(g\), roughly the maximum to be expected on a dry road for a well-maintained family car. Since from Newton’s second law of motion, force equals mass times acceleration, we can write
(3)
\[\begin{equation} Q \quad = \quad M \times bg \end{equation}\]where \(M\) is the mass of the vehicle. How is this force generated? As we’ve already observed, the braking system on a car does its work indirectly. It doesn’t grab the road, it grabs the wheels. A torque is applied to each wheel so that it resists turning. If the braking torque at any given wheel is \(T\) say, and the wheel radius \(r\), the result is a tangential force \(T/r\) at the contact patch that provides resistance to forward motion. Ideally, the braking force contributed by each wheel should be just equal to the peak friction force that the tyre/road interface can handle. Any more, and the wheel will slide, leading to loss of control. Any less, and the tyre will have spare braking capacity. Either way, the system will fail to exploit all the available braking force, with obvious consequences for the stopping distance.
The target is to achieve peak friction at each tyre simultaneously, so that the total braking force is equal to \(\mu\) times the total normal contact force \(Mg\). This is the maximum theoretical braking force, and we’ll denote it by \(Q_{max}\):
(4)
\[\begin{equation} Q_{max} \quad = \quad \mu \times Mg \end{equation}\]If we compare the right-hand side of equation 3 with the right-hand side of equation 4, we see that the maximum possible deceleration, expressed in multiples of \(g\), is numerically equal to the friction coefficient \(\mu\).
Effect of unequal axle loads
Life would be simple for the engineer if the car had only one axle. With two axles, the braking forces are harder to manage because the loads on the axles are rarely equal. When standing still, the weight of a front-wheel drive car of mass \(M\) is distributed typically in the ratio 60:40 between front and rear. This means that the load on the front axle is \(0.6 Mg\) newtons, and that on the rear \(0.4 Mg \;\) newtons. The distribution changes according to the number of people and the amount of luggage on board. Hence it changes from trip to trip. Worse, it changes from moment to moment owing to load transfer whenever the driver accelerates or applies the brakes (Section C2009).
To see why this matters, it is helpful to picture an experiment in which a car goes through a series of braking tests on a level surface. In each case it decelerates at a steady rate \(bg\), with \(b\) fixed at a different value for each test. We will assume the wheelbase is 2.5 m, and that the centre of mass is 0.5 m above the road surface. Since the front wheels carry more weight, they can generate more friction, and it would be logical to configure the hydraulics so they develop a higher braking torque. For the sake of argument, we’ll fix the braking force distribution at 75:25, so that from equation 3 the braking forces delivered through the front and rear axles will be respectively
(5)
\[\begin{equation} Q_{f} \quad = \quad 0.75Mbg \end{equation}\](6)
\[\begin{equation} Q_{r} \quad = \quad 0.25Mbg \end{equation}\]The set-up is illustrated in figure 6. But equation 5 is valid only up to the point where the axle concerned reaches peak friction and the wheels lock. The peak friction in turn is determined by the coefficient of friction \(\mu\) and the normal contact force on that axle. A corresponding proviso holds for equation 6. So now, we must work out the normal contact forces.
Figure 6
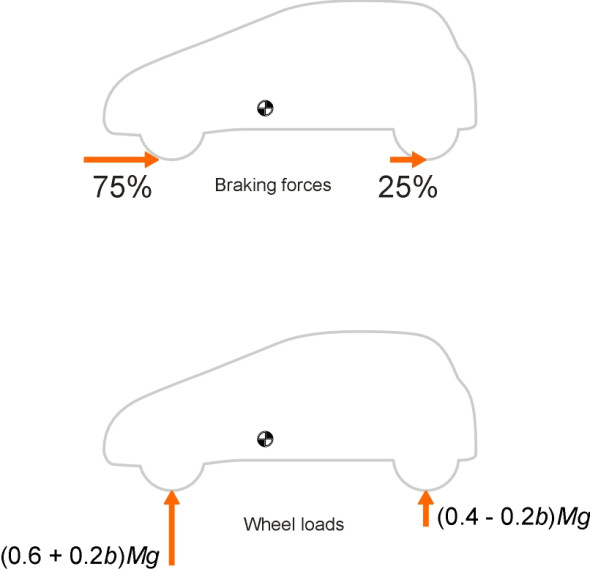
Since the braking forces act horizontally through the tyre contact patches, together they exert a couple about the car’s centre of mass equal to \((0.75 Mbg + 0.25 Mbg) \times 0.5 = 0.5 Mbg\) Nm. This couple is balanced by a transfer of vertical load between the front and rear axles. The front axle carries an additional load of \(0.5 Mbg / 2.5 = 0.2 Mbg\) N, while the rear axle load is reduced by the same amount. The total loads for the two axles are therefore
(7)
\[\begin{equation} P_{f} \quad = \quad (0.6 \; + \; 0.2b) Mg \end{equation}\](8)
\[\begin{equation} P_{r} \quad = \quad (0.4 \; - \; 0.2b) Mg \end{equation}\]Now we can determine limits on the braking forces separately for each axle. If the coefficient of friction between each tyre and the road is \(\mu\), then the maximum braking force \(Q_{f,max}\) available from the front axle is equal to \(\mu\) times the normal contact force \(P_{f}\), so
(9)
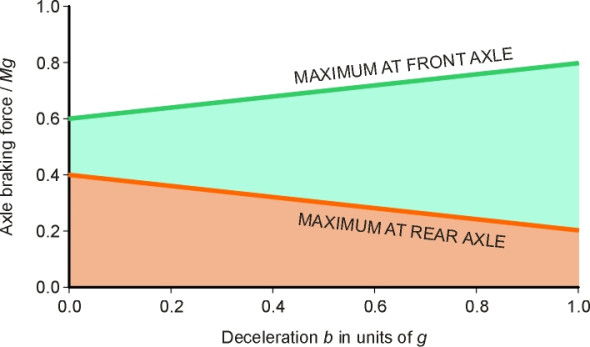
\[\begin{equation} Q_{f, max} \quad = \quad \mu (0.6 \; + \; 0.2b) Mg \end{equation}\]and similarly for the rear axle
(10)
\[\begin{equation} Q_{r, max} \quad = \quad \mu (0.4 \; - \; 0.2b) Mg \end{equation}\]The two curves are plotted in figure 7 against \(b\), assuming a good quality surface whose coefficient of friction \(\mu\) is equal to 1.0. These, remember, are upper limits (and they apply only to a car with the particular dimensions we assumed earlier). The actual braking forces depend on how hard the driver presses the brake pedal and on how the braking forces are split between the two axles. As previously set out in equation 5 and equation 6, they are respectively \(0.75 Mbg \;\) and \(0.25 Mbg\).
Figure 7
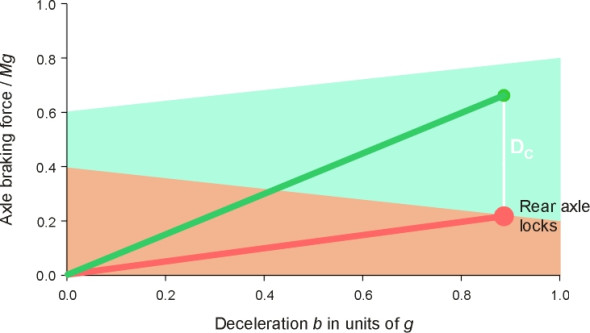
Now we can picture what happens in our experiment. The driver doesn’t actually need to stop the car: the aim is to see how it responds to different levels of brake pedal pressure. In the first test, the driver presses the brake pedal gently and holds that pressure so the car experiences a mild deceleration. The deceleration is represented by the leftmost coloured circles in figure 8. The green circle shows the braking force at the front axle and the red one the braking force at the rear axle. In the next experiment, the driver presses the brake pedal a little harder, and the car decelerates more sharply, at a level represented by the two circles further over to the right hand side of figure 8. The front and rear braking forces are larger but otherwise nothing unusual happens. The experiment continues in this fashion, with the driver pressing the brake pedal a little harder on each occasion so the braking forces at the front and rear axles increase from one test to the next. Their values in successive tests are traced out by the two heavy lines labelled respectively ‘FRONT’ and ‘REAR’ in figure 8. Everything is fine until the deceleration reaches a critical level as shown in figure 9. At this point, the braking force demanded of the rear axle just exceeds the maximum of which it is capable, and the rear axle locks. For reasons explained in Section C0415 the car spins out of control. This condition terminates the experiment.
Figure 8
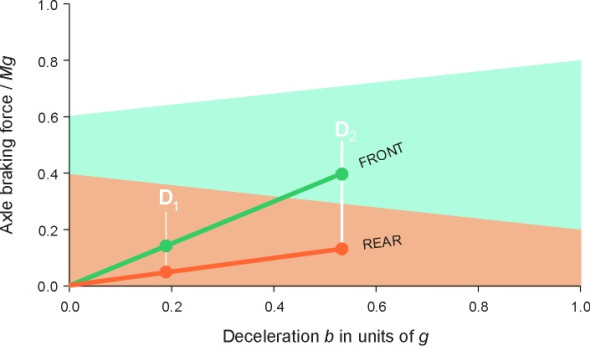
Figure 9
A dilemma
What did the experiment reveal? On this occasion, the maximum deceleration of which the car is capable (given the static loads and the proportioning of braking effort between front and rear) occurs at the intersection of the line representing actual rear axle braking force with the maximum rear axle braking force. By comparing equation 6 with equation 10 it is not difficult to show that the point of intersection occurs at a deceleration of \(0.89 g\). Since the coefficient of friction \(\mu\) was fixed at 1.0, we know from equation 5 that the maximum theoretical deceleration is \(1.0 g\). Our braking system has therefore peaked at a value around 89% of the maximum. It has achieved an efficiency of 89%.
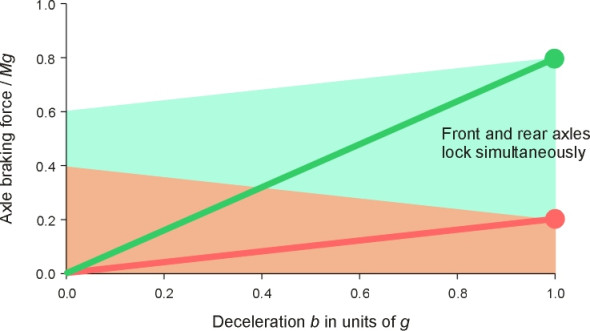
How can we improve this result? Since the rear wheels lock first there must be some spare braking capacity at the front, so we re-configure the hydraulics at 80:20. As shown in figure 10, this produces a better result, with both axles locking simultaneously, to give a peak deceleration of \(1.0 g\) and an efficiency of 100%.
Figure 10
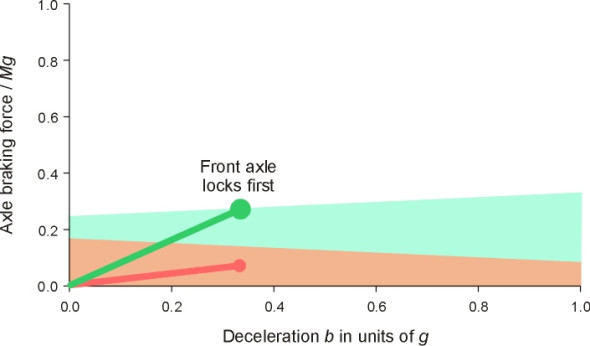
But will this proportion work on all types of road surface? As a final check, we now test the car on a wet road with a coefficient of friction \(\mu\) of 0.4. This time, a braking force distribution of 80:20 is too heavily biased towards the front axle. Why? Because on a slippery surface the maximum braking force overall is reduced, and less load is transferred from rear to front, as shown in figure 11. This time, the front axle locks up first, at a deceleration of \(0.33 g\) and efficiency of only 83%! Hence the optimum proportioning of braking effort varies not only with the arrangement of passengers and luggage in side the car, but also with the quality of the road surface.
Figure 11
Brake proportioning
For many years this has presented car engineers with a headache. Individually, the hydraulics, the brake pads and the tyres may be fine but the system as a whole doesn’t necessarily achieve its potential. The losses can be quite large, and legislators have tried to regulate vehicle design and construction so as to guarantee acceptable braking performance across a range of conditions. The main aim is to make the front wheels lock first. Further requirements are expressed in terms of the ‘Adhesion utilisation diagram’, which sets minimum standards for the proportion of tyre/road friction that is exploited under varying road conditions and varying load conditions [4]. Engineers have developed a number of devices to achieve these goals, including
- a pressure-limiting valve that reduces braking effort at the rear wheels
- a ‘deceleration-conscious’ valve that modifies the balance according to the measured g-force
- a ‘load-conscious’ valve that senses load transfer.
Load-conscious valves are particularly useful for heavy vehicles, where the static load distribution can change radically from one trip to the next. Details of these and other devices can be found in [7] [10] [15] [23].
Anti-lock
In principle, the problem of brake proportioning has been side-stepped with the development of anti-lock braking systems that operate independently on each wheel. The variety found on most cars today was pioneered by Bosch under the name Anti-Blockierung System, or ABS for short. It senses when a wheel is about to lock up, and momentarily overrides the driver’s braking action on that wheel so that it continues to turn. The cycle of brake application and release occurs at a rate of up to 15 times per second. Effectively, the system allocates the braking effort between all four wheels according to the friction available from each wheel at each moment, an enormous advantage in an emergency, allowing even an inexperienced driver to extract all the available grip from a road surface. ABS systems are now commonly supplied on both passenger cars and heavy vehicles. Further details can be found in [11] [17] [24].
However, the matter is not entirely settled. ABS systems are relatively complicated and expensive, and they involve added weight because a separate hydraulic pump is needed to re-apply the disk pad at the end of each release cycle. For the smaller, cheaper cars that will dominate in tomorrow’s developing world, other solutions may emerge. For electric cars, on the other hand, the solution will be more straightforward. Electric motors can be made to operate regeneratively, so that when the driver presses the brake pedal they slow the wheels down and re-charge the batteries at the same time. With a motor buried in each wheel hub, sensors can switch the braking on and off independently at each of the four wheels and thereby reproduce the effect of ABS braking in more direct fashion with fewer mechanical components to go wrong.