R.0415
Curving
In principle, a train can guide itself around curves in the track without the wheel flanges touching the rails. Described in Section R1610, the principle is more than 150 years old. But it only works when the vehicle is moving slowly and the curve is not too sharp, otherwise the situation is more complicated. On real track, a vehicle will occasionally jump the rails, and it took the combined efforts of mathematicians, scientists and engineers over a hundred years to understand why. In the meantime, railway managers learned how to align the track and operate services largely on the basis of experience punctuated by the occasional dramatic failure. Without a real understanding of the interplay between wheel and rail, progress was slow and uncertain. What was the smallest radius of curve that a train could negotiate? How fast could it do so without damaging the rails or flying off the track? In this Section we shall try to describe the theory and some of the practical implications that arise from it.
Wheelset guidance
We start by imagining a wheelset rolling along a track, and for the moment, ignore the rest of the vehicle. There is room for the wheelset to shift from side to side over a small distance because the flanges fit loosely between the rails. In Section R1610 we showed that on a straight track, when displaced laterally by a distance \(y\) from its central or ‘reference’ position, a wheelset will follow a path that initially curves back towards the track centreline. The radius \(R\) of its path is given by
(1)
\[\begin{equation} R \quad = \quad \frac{wr}{2\gamma y} \end{equation}\]where \(\gamma\) is the half-cone angle, \(w\) the track width, and \(r\) the tread radius. Let us now turn the situation on its head and picture wheelset rolling on a curve of radius \(R\). It will follow the curve accurately without any assistance provided it can maintain a constant displacement \(y\) away from the track centreline, the displacement \(y\) being given by rearranging equation 1 thus:
(2)
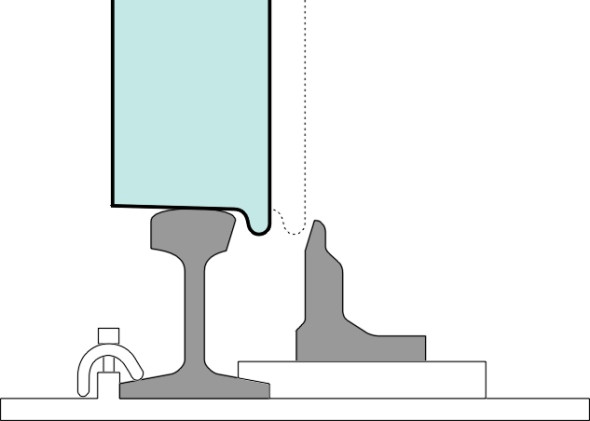
\[\begin{equation} y \quad = \quad \frac{wr}{2 \gamma R} \end{equation}\]The smaller the curve radius, the larger the displacement needed. But the displacement is limited by the clearance between the flange of the inside wheel and the shoulder of the rail on which it runs, measured with the wheelset in its reference position. This clearance is known as the flangeway clearance\(\,\) (figure 1). It mustn’t be too large otherwise the flange won’t pass through gaps in the rail at turnouts and crossings (figure 2). In any case, you don’t want the vehicle body to shift from side-to-side for more than few millimetres because it might foul trackside equipment or even a station platform. The maximum flangeway clearance is usually fixed in the range 7 - 10 mm [8].
Figure 1
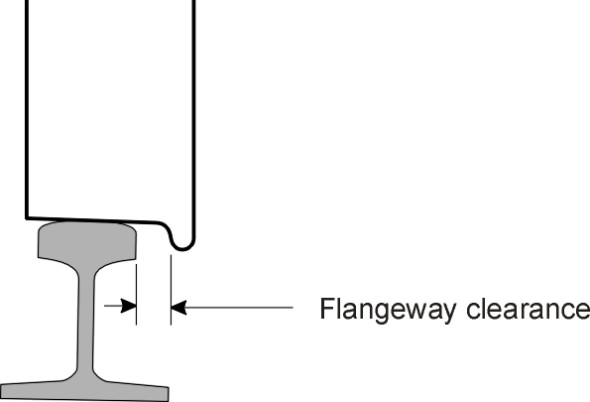
Figure 2
If we denote the flangeway clearance by \(y_{\max}\), we can deduce the minimum curve radius \(R_{\min}\) as being given by the formula
(3)
\[\begin{equation} R_{\min } \quad = \quad \frac{wr}{2 \gamma y_{\max }} \end{equation}\]The formula has been known to railway engineers since the late nineteenth century [21]. It represents the smallest radius that the wheelset can negotiate without the flange touching the inside face of the outer rail. Let’s substitute some plausible values for the quantities on the right hand side, say, \(w = 1.5\) m, \(r = 0.5\) m, \(\gamma = 0.05\), and \(y_{\max} = 8\) mm. The minimum curve radius then comes to a little over 900 m. For a shallower cone angle 1/40 typical of European and Japanese high-speed railways, the minimum radius doubles to nearly 2 000 m. A curve of radius less than 1000 m is usually classified as a ‘sharp’ curve [25].
Behaviour on sharp curves
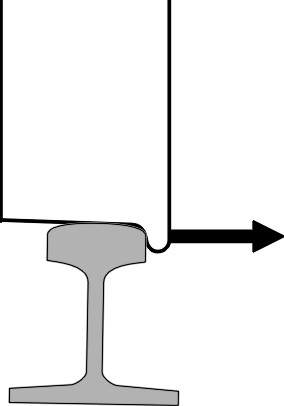
So how does the wheelset behave when it encounters a curve of radius less than 1000 m? To keep things simple, let’s assume that the wheelset is correctly aligned so its projected centreline passes through the centre of the curve, in other words, it has a radial alignment (figure 3). Since the natural tendency of the wheelset is to follow a wider curve than that presented by the rails, two things happen. First, the outer wheel flange will run up against the rail shoulder (figure 4), and the wheelset is compelled to follow the track curvature by a horizontal flanging force\(\, F\). Secondly, the rolling radius of the outer wheel is no longer compatible with that of the inner wheel: it is no longer sufficient to drive the outer wheel through the extra distance that it must travel between the start and finish of the curve. Either the radius of the inner wheel is too large, or the radius of the outer wheel is too small. If we assume for the sake of argument that the inner wheel remains firmly locked to the rail surface, then outer wheel must slide along the rail - there is a mismatch between the speed at which the rail surface and the tread surface flow through the contact patch.
Figure 3
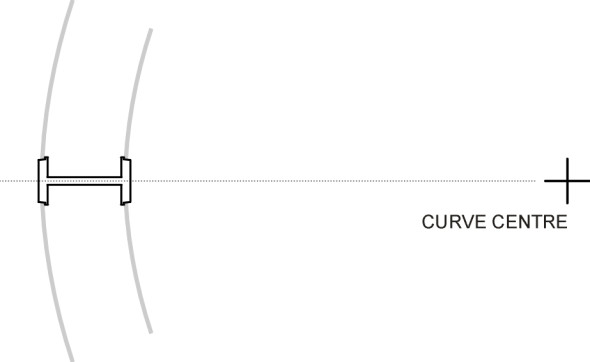
Figure 4
Actually, the term ‘slide’ is not quite right here. If the mismatch is small, the difference in speeds will be modest, sufficiently modest to be taken up by creep so that sliding only takes place over part of the contact area. But if the mismatch is larger, we say that the creep becomes ‘saturated’ and full sliding friction occurs across the whole contact patch. In either case, there is a tangential shear force in a longitudinal direction that resists the progress of the outer wheel, dragging it rearward (figure 5). So what about the inner wheel? As a first approximation, one concludes that if the friction at the wheel bearings together with any frictional torque arising from the outer wheel flange grinding against the rail is small enough to be neglected, there can be no net torque acting on the axle, and there must be an equal force acting on the inner wheel in the opposite direction, dragging it forward (figure 5).
Figure 5
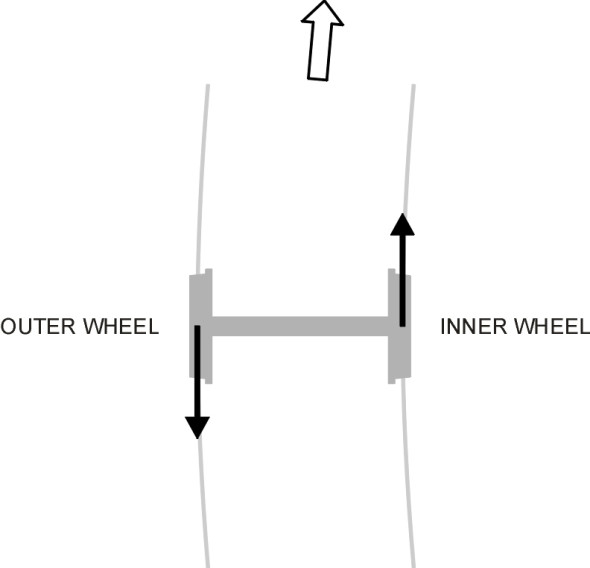
There are other friction forces that don’t arise in this artificial set-up, but if we are prepared for the moment to ignore them we can calculate the value of the longitudinal component. Let’s assume that the vertical wheel loads have equal values denoted by \(P\), say. If the coefficient of sliding friction is denoted by \(\mu\), then for a curve sufficiently sharp to induce saturation, each wheel experiences a friction force equal to \(\mu P\). Given a coefficient of friction of 0.2 and a typical wheel load of 10 tonnes (roughly 100 kN), its value would be 20 kN - a considerable force that must be catered for in the design of the vehicle and track. Of course this is a hypothetical exercise because in reality, there is no such thing as an isolated wheelset. But it will turn out to be useful when we look at multi-axle vehicles later. Note that if the curve is sharp enough to induce full sliding, the magnitude of the friction force is independent of the speed at which the wheelset is travelling, and independent of the radius of the curve.
Figure 6
The worn wheel profile
So far, we have assumed that the tread surfaces are perfectly conical. This implies a simple relationship between lateral displacement and rolling radius: when a conical wheelset deviates to the left, say, the left-hand wheel will rise on the rail surface so that its effective rolling radius increases linearly with displacement \(y\), the increase being equal to \(\gamma y\) where \(\gamma\) is the cone half-angle in radians. The right hand wheel will at the same time have its rolling radius reduced by a similar amount. The difference in rolling radius \(\Delta r\) between the two wheels is therefore given by
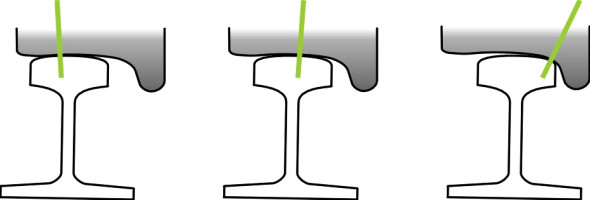
(4)
\[\begin{equation} \Delta r \quad = \quad 2 \gamma y \end{equation}\]But in reality, railway wheels are rarely conical. When it first goes into service, the geometry of a truly conical wheelset deteriorates more quickly than one might suppose. Because the contact area is small, there are high local stresses, so that the tread and upper surface of the rail are ground towards a common profile. The tread surface is hollowed out, and the angle at which it meets the rail surface is not a constant. Instead, it varies with the deviation of the wheelset from its central position. As figure 6 shows, it is large at the flange root and decreases almost to zero, sometimes becoming negative, at the outer face of the wheel. This rapid deterioration of the conical profile makes matters awkward for the analyst, because it undermines the assumptions on which vehicle dynamics are modelled. On the other hand, one can reverse the logic and treat equation 4 as way of defining equivalent conicity in terms of the change in rolling radius instead. This equation can be arranged in the form
(5)
\[\begin{equation} \gamma \quad = \quad \frac{\Delta r}{2y} \end{equation}\]Thus for any given lateral displacement of a non-conical wheelset we can stipulate [11]:
(6)
\[\begin{equation} \gamma_{\text{equivalent}} \quad = \quad \frac{\Delta r}{2y} \end{equation}\]The formula can be used to estimate equivalent conicity of real wheels from measurements of the tread profile. The results may come as a surprise. With only a modest degree of wear, the value of the equivalent conicity is not only larger than the nominal 1:20 or 1:40 one might expect, but many times\(\,\) larger. With wear, the profile tends to stabilise at a value of 0.2 to 0.3 [3].
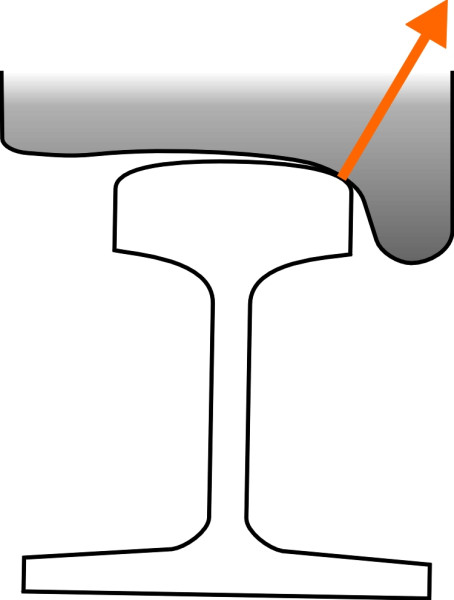
However, provided the wear is kept within certain limits, a hollow profile has at least one practical benefit. As the distinction between tread and flange becomes blurred, there is a greater differential between the rolling radii at any given lateral displacement, and steering round sharp curves improves. A train with worn wheels can negotiate a curve of radius down to about 150 m and still remain within the flangeway clearance [23]. Also, the normal contact force between wheel and rail contributes directly to guidance (figure 7).
Figure 7
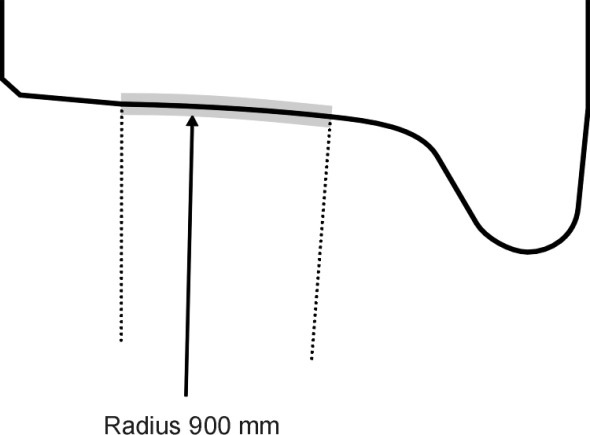
All of this raises the question of whether a conical profile is actually the right profile in the first place. It has been found in practice that a wheelset will perform longer in service if it is given a curved profile from new. This step was first taken in the UK during the early 1960s [11] [26], and nowadays many railways have standardised on a ‘worn’ wheel profile. For example in Europe, the S1002 wheelset is machined during manufacture to a hollow form and used in conjunction with the UIC 54 rail, which usually has an inclination of 1:40 [2]. The cross-sectional profile of a wheel widely used in Japan [9] follows a circular curve of radius 900 mm across the main contact area (figure 8).
Figure 8
The rigid frame
Up to now we have pictured the wheelset moving in perfect radial alignment. This is a hypothetical picture: most wheelsets are attached to a frame that to a greater or lesser extent prevents them from swivelling to take up curvature in the rails. Some vehicles provide more flexibility than others. For example, many freight wagons have three-piece bogies whose axle-boxes are free to move a couple of millimetres fore-and-aft in their mountings. Others have resilient mountings that allow for movement against a spring-like resistance. But any constraint tends to place the leading outer wheel at an angle to the rail as shown in figure 9, and the longer the wheelbase, the larger the angle. This angle is called the angle of attack, and other things being equal, the larger the angle of attack, the more likely it is that the wheel will ride up the rail shoulder and cause a derailment, a point to which we’ll return later in Section R0314.
Figure 9
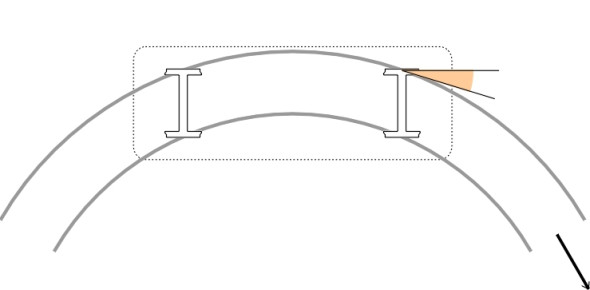
Steam locomotives
Steam locomotives face another difficulty. Since the driving wheels are joined by connecting rods on either side, they are effectively clamped in position, unable to yaw relative to the frame and unable to take up a radial alignment, although of course they can move up and down on their suspension springs. During the early nineteenth century, most mainline steam locomotives had three driving wheelsets mounted on a rigid frame. There was frequent flange contact, and derailments were common, so the question arose how to reduce the severity of the impact between the wheel and the rail, particularly on sharp curves. For many years it was believed that the underlying cause was the simple and obvious one: centrifugal force. If you drive a car round a curve at gradually increasing speed, the friction between the wheel and road surface will eventually fall short of the amount needed to hold the vehicle on a curved path and it will skid sideways until the tyres hit the kerb. Similarly when friction is exhausted the flanges of the outer wheels of a railway vehicle will strike the shoulder of the rail.
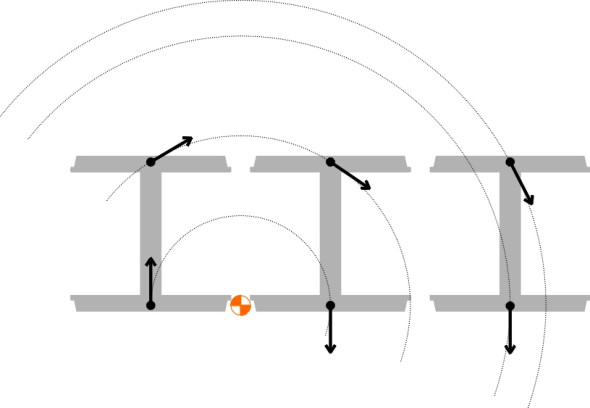
But this didn’t explain why derailments often occurred at relatively low speeds in freight yards and maintenance depots. The cause was discovered by chance during an experiment with a steam locomotive in 1883, which ran off the rails almost at walking pace. The loco had six driving wheels set in a rigid frame. The engineer in charge of the experiment, J Mackenzie, observed that the leading outer wheel climbed the rail first and deduced that it was forced to do so by the combined actions of the other five, which were straining against the curvature and tended to push the vehicle straight ahead. It appeared that on a sharp curve, the self-steering effect of the conical treads was insufficient, and that the leading outer wheel was actually sliding on the rail surface. In fact, the treads of all six wheels were both rolling and sliding simultaneously, the directions of slip in each case being at different angles to the direction of motion, rather like a six-legged table skating across a polished wooden floor. The six angles were consistent with a notional ‘centre of friction’ which he believed was located on the inside rail as shown in figure 10. The arrows show the direction in which the wheels are sliding on the rail surface. Other investigators put the theory on a sound mathematical basis and established the directions of sliding together with the friction forces involved. Although differing in detail, each study confirmed that the friction forces conspired together to produce a large flanging force between the leading outer wheel and rail shoulder.
Figure 10
How can the flanging force be predicted? The problem is technically difficult because it involves a set of non-linear simultaneous equations that can only be solved using successive approximations [5]. But we can demonstrate the principles using a simplified model. Picture a small tank engine of the kind you might find on a ‘heritage’ steam railway today, with two driving axles, and a connecting rod on either side. Figure 11 shows diagrammatically the four wheels in plan view together with the forces acting on them at their respective points of contact with the rails. We assume the wheel treads are cylindrical and that full sliding occurs between each wheel tread and the rail surface, so the resultant forces are all equal to \(\mu P\), where \(\mu\) is the coefficient of sliding friction and \(P\) the wheel load. If the curve is sufficiently sharp, the trailing inner wheel will contact the inner rail shoulder as well, but here we’ll assume this is not the case. The flanging force at the leading outer wheel is denoted by \(Y\). The wheelbase is \(2 a\) and the track width between contact centres \(2 b\).
Figure 11
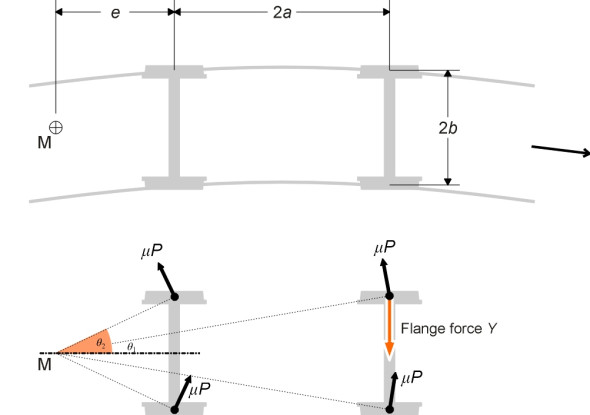
Given that the wheel loads are equal and there is no traction (the loco is coasting freely along) it can be shown that the centre of friction M lies towards the rear of the vehicle on its centreline [5]. Denote the distance of the centre of friction measured aft of the trailing axle by \(e\). Then referring to figure 11, if we resolve forces in the radial direction we get
(7)
\[\begin{equation} Y \quad = \quad 2 \mu P \cos {\theta_1} \; + \; 2 \mu P \cos {\theta_2} \end{equation}\]where
(8)
\[\begin{equation} \cos {\theta_1} \quad = \quad \frac{2a + e}{\sqrt {{\left( {2a + e} \right)}^2 \; + \; b^{2}}} \end{equation}\](9)
\[\begin{equation} \cos {\theta_2} \quad = \quad \frac{e}{ \sqrt {e^{2} \; + \; b^{2}}} \end{equation}\]which if we substitute in equation 7 and rearrange the result, leads to
(10)
\[\begin{equation} \frac{Y}{\mu P} \quad = \quad \frac{2 \left( {2a + e} \right)}{\sqrt { {\left( {2a + e} \right)}^2 \; + \; b^{2}}} \; + \; \frac{2e}{ \sqrt { e^{2} \; + \; b^{2}} } \end{equation}\]And taking moments about M:
(11)
\[\begin{equation} (2a + e) Y \quad = \quad 2 \mu P \sqrt {{\left( {2a + e} \right)}^{2} \; + \; b^{2}} \; + \; 2 \mu P\sqrt {e^{2} \; + \; b^{2}} \end{equation}\]so that
(12)
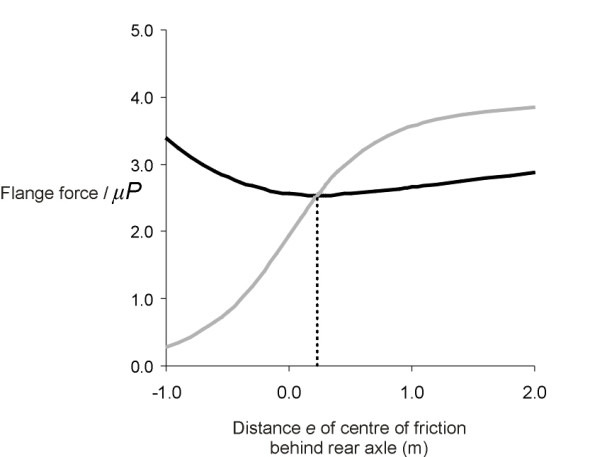
\[\begin{equation} \frac{Y}{\mu P} \quad = \quad \frac{2}{(2a + e)} \left\{ \sqrt {(2a + e)^{2} \; + \; b^{2}} \; + \; \sqrt {e^{2} \; + \; b^{2}} \right \} \end{equation}\]Equations equation 10 and equation 12 together form a pair of simultaneous equations for the two unknowns \(e\) and \(Y\). In principle we can eliminate \(Y\) and obtain a single equation for \(e\). But for any particular case it is easier to solve the equations graphically. We shall plot the right-hand side of equation 10 as a function of \(e\) and similarly the right-hand side of equation 12, together on the same graph. The value of \(e\) can then be read off where the two curves cross. For a loco whose wheelbase is 3.0 m and track width 1.5 m, we have \(a\) = 1.5 m and \(b\) = 0.75 m. Plots of the two curves are shown in figure 12, from which we read off the solution \(e = 0.2\) m and \(Y / \mu P = 2.5\) approximately. So if we take the coefficient of sliding friction \(\mu\) as 0.2, and the vertical load \(P\) on each wheel as 10 tonnes, the flanging force \(Y\) works out at just under 50 kN. It’s not a standard term, but we’ll call it the friction flange force\(\,\) to distinguish it from any centripetal force that might arise from inertia if the loco were travelling round the curve at speed.
Figure 12
How to steer a steam locomotive
As we shall see in Section R0314 it is flanging forces of this kind that can prise the leading outer wheel off the rail even when the vehicle is barely moving. How then could a steam locomotive be configured to steer through sharp curves without risking derailment and without damaging the track? Towards the end of the 19th century, engineers found two ways of doing this. The first was to support the front of the chassis on a ‘pony truck’, an extra wheelset located ahead of the driving wheels that carried some of the weight (figure 13). It was pivoted at a point well aft of the axle centreline so it followed the curvature of the rails, and its motion was resisted either by a spring, or alternatively by the weight of the boiler, which rested on sliding bearings aligned in a shallow ‘vee’ laterally across the pony truck frame. In either case, the reaction guided the front of the locomotive into the curve. Many steam locos were fitted additionally with carrying wheels at the rear.
Figure 13
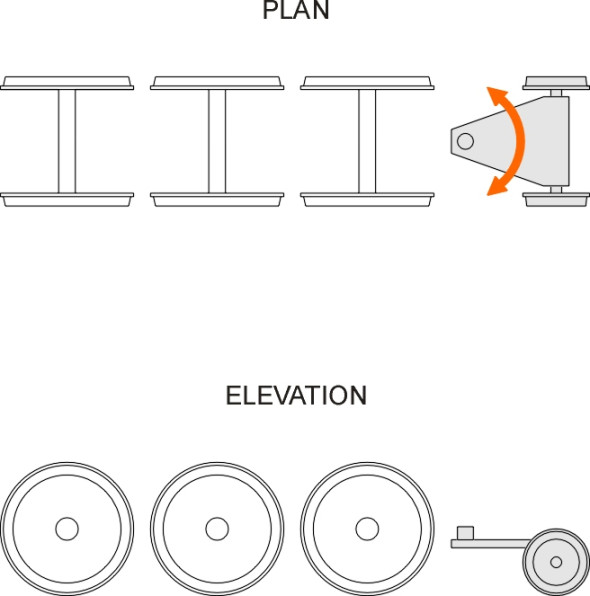
Figure 14
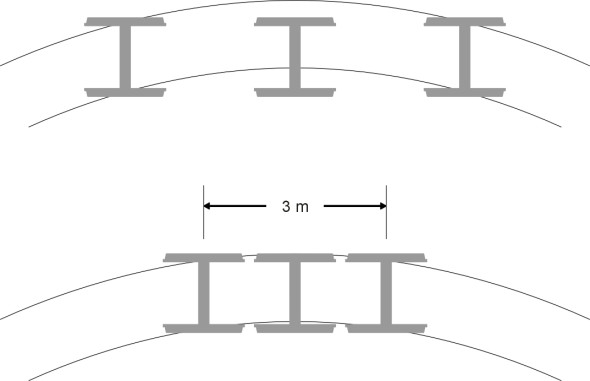
Figure 15
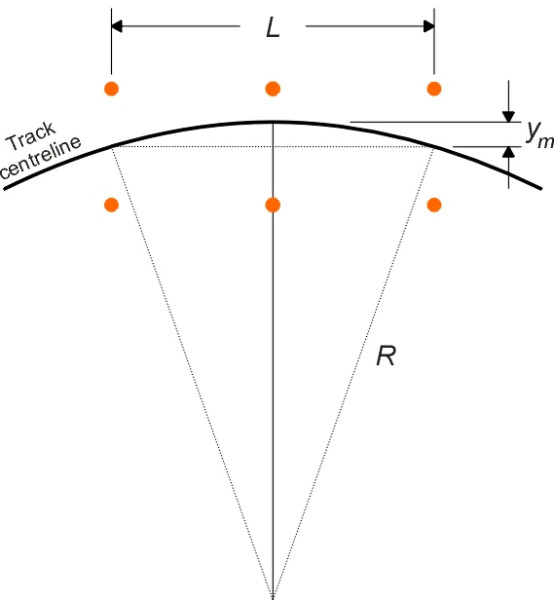
The second method was to group the driving axles together as closely as possible, which minimised the angle of attack at the leading wheelset and also brought the three axles more closely into alignment with the rails (figure 14). For a locomotive with six driving wheels each of 2 m in diameter this meant a rigid wheelbase of a little over 4 m. If you picture a six-wheeled configuration on a sharp curve you’ll see that the treads of the middle wheelset do not lie on the crown of the rail, and therefore it was common practice to provide some flexibility for the axle in the centre to undergo lateral displacement relative to the other two, typically up to 25 mm [19]. Applying the well-known Chord theorem for a circle we see from figure 15 that
(13)
\[\begin{equation} y_{m} ( 2R - y_{m} ) \quad = \quad \left( {\frac{L}{2}} \right)^{2} \end{equation}\]where \(R\) is the curve radius, \(y_{m}\) is the maximum displacement of the middle wheelset, and \(L\) the wheelbase between the leading and trailing axles. This equation can be re-arranged to give approximately
(14)
\[\begin{equation} R \quad \approx \quad \frac{L^{2}}{8y_{m}} \end{equation}\]which for a 25 mm displacement and a 5 m wheelbase yields a minimum curve radius of about 150 m. There was another way of dealing with this particular form of misalignment, which is still applied to model train sets today. It was to remove the flanges entirely from the middle wheelset, and if necessary to widen the tread so that part of it would always be resting firmly on the rails.
Bogie steering
We have seen that a wheelset mounted rigidly on a vehicle frame doesn’t line up properly with the rails when the vehicle goes round a curve. The misalignment is worse for a vehicle such as a passenger coach that has a long wheelbase. The solution for passenger coaches was pioneered in the USA where sharp curves and kinks in the track were once common. It was to mount the wheelsets on bogies, one at each end of the body frame (figure 16). This is the configuration used on most high-speed rolling stock today, including electric locomotives and a large proportion of the freight wagon fleet. A bogie is almost a vehicle in its own right, but one with a modest wheelbase of around 3.0 m, which is the standard for example on Thalys, TGV, and Eurostar trains [4].
Figure 16
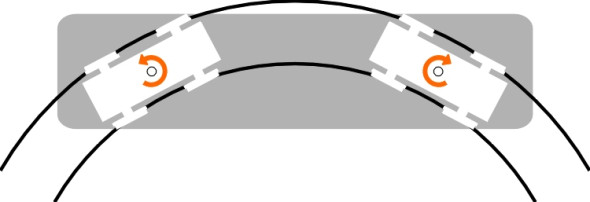
Figure 17
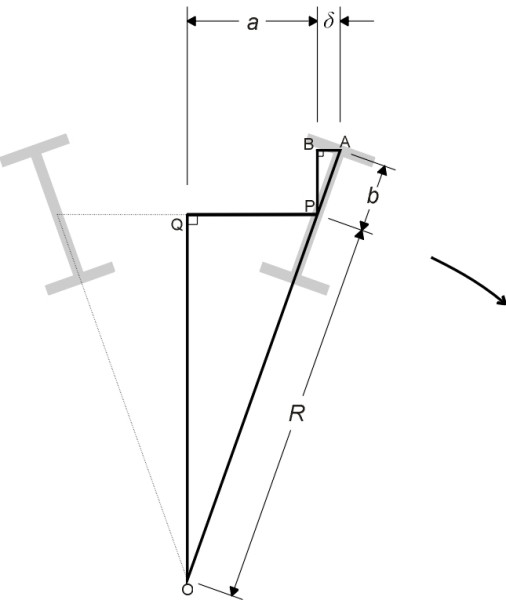
Curving behaviour
Having a short wheelbase, the bogie reduces the angle of attack on curves. The angle can be reduced further if the axles are free to swivel or yaw relative to the bogie frame, or what amounts to the same thing, if each axle box can move fore-and-aft within its mounting. By how much? figure 17 shows the axles of a bogie taking up a radial alignment on a curve of radius \(R\) (the wheelset yaw is exaggerated). The wheelbase is \(2 a\) and the track width \(2 b\). The leading outer wheel has shifted forward a distance \(\delta\) relative to the bogie frame, and the inner wheel rearwards by the same amount. Since triangles PAB and OPQ are similar, the ratio of AB to AP equals the ratio of PQ to OP. It follows that
(15)
\[\begin{equation} \frac{ \delta }{a} \quad = \quad \frac{b}{R} \end{equation}\]so that
(16)
\[\begin{equation} \delta \quad = \quad \frac{ab}{R} \end{equation}\]If the bogie has wheelbase 3.0 m and the track width between contact centres is 1.5 m, on a curve of radius 1000 m the leading outer wheel would need to move forward a distance of \(1.5 \times 0.75 / 1000 \times 1000 = 1.125\) mm in order to take up a radial alignment. Hence the total movement required at each axle-box is about \(\pm{}\) 1 mm, and more on sharper curves. It is also helpful to allow a degree of lateral shift so that each axle can move independently from side to side relative to the bogie frame to take up the kinks in poorly aligned track.
Figure 18
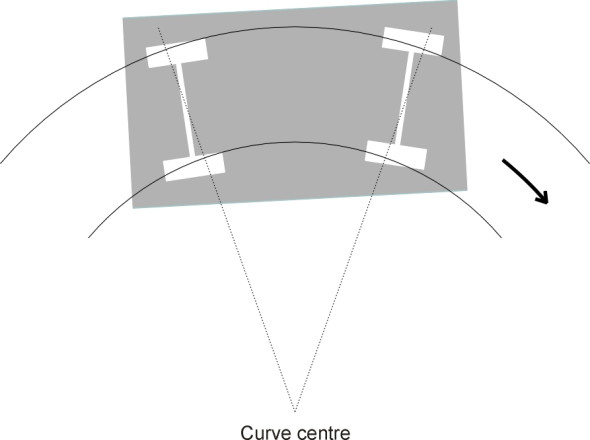
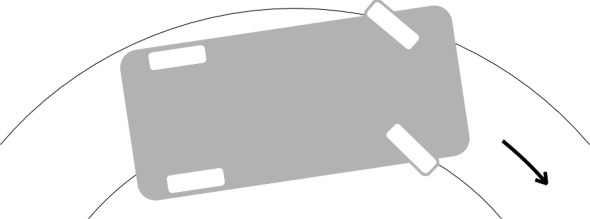
Freedom of movement is provided in different ways on different kinds of vehicle. In some cases there may be a gap between the axle-box and the frame so that while there is little resistance to yaw, the degree of yaw is limited to a defined range, as is the case with some three-piece freight bogies for example. There may also be some clearance laterally, allowing for lateral displacement. In other cases, for example on most passenger coaches, the axle boxes are mounted in rubber bushes so that a degree of yaw and a degree of lateral displacement is permitted, albeit against a spring-like resistance. Any resistance implies that on a curve, the wheelsets will yaw to some degree, but not enough to achieve radial running. At this point, the geometrical relationship between the bogie frame, the wheels, and the track becomes more complicated and nowadays, computer packages are used to explore what is going on. Figure 18, based on [22], shows diagrammatically what happens to a bogie moving on a sharp curve (the angles and displacements are deliberately exaggerated). The geometry can change according to the curve radius and the cant deficiency amongst other things, but in this example, the leading wheelset yaws outwards relative to the rails as if trying to steer the bogie away from the centre of the curve. This makes an interesting comparison with the behaviour of an automobile, where the front wheels always yaw in the opposite direction, towards the centre (figure 19).
Figure 19
What about the forces between the wheels and the rails? They too vary from case to case, but when flanging occurs, it bears primarily on the leading outer wheel [13] [18]. Earlier we investigated the flange force produced at low speeds by a steam locomotive together with the damage it can cause. Much the same applies to a modern electric locomotive. On a 300 m curve, the leading wheelset of either bogie produces a flanging force of about 50 kN or so, and on a poorly aligned track it will fluctuate randomly above and below this value [14]. Not surprisingly, the International Union of Railways (UIC) recommends a maximum limit on lateral guiding forces. For a track designed to carry a load of 22.5 t per wheelset, equivalent to about 220 kN, the limit is 60 kN [15]. This means that very roughly, the track is expected to resist a lateral load up to a quarter of the vertical load.
The wheels of a train, incidentally, experience another force that we haven’t mentioned so far. It arises on sharp curves when they are not precisely aligned with the rails. The flanging forces have an additional component \(S_{cr}\) that acts as a drag on the vehicle’s forward progress, a form of rolling resistance if you like, and although normally small it increases greatly on sharp curves and can be significant for freight trains. There is a widely-used empirical formula for predicting its value in newtons per tonne of loaded wagon mass on a curve radius \(R\) measured in metres:
(17)
\[\begin{equation} S_{cr} \quad = \quad \frac{6116}{R} \end{equation}\]So for a wagon of 40 tonnes gross on a curve of radius 200 m the resistance is \((40 \times 6116) / 200 = 1.2\) kN. The resistance is thought to double approximately when the train stops [1]. If in addition the track is canted, the flanges of the inner wheels will press against the inner rail, so that if a freight train stops on a sharp curve, it may be difficult to get it going again.
Steering and stability
So the modern bogie provides some flexibility for the wheelsets to swivel, but not enough to eliminate the ‘angle of attack’ of the leading outer wheel against the rail shoulder. Why not dispense with restraints and leave the wheelset free to yaw into a perfect radial alignment? As we saw in Section R0418, a lightly restrained wheelset is prone to ‘hunt’, and indeed hunting oscillations can occur at different levels within the assembly as a whole, including the bogie. For a bogie, the critical speed at which the oscillations start is controlled by two factors [12] [24]:
- the ‘shear stiffness’ or resistance to relative lateral displacement of the axles, and
- the ‘bending stiffness’ or resistance to relative yaw between the two wheelsets.
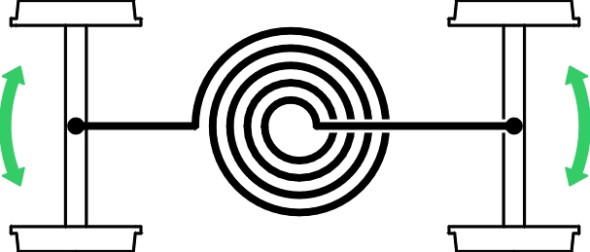
The shear stiffness requirement can be represented by a lateral spring connecting the two wheelsets as shown in figure 20. The yaw stiffness can be represented by a spiral spring (figure 21). In practice, an engineer wouldn’t actually fix springs to the wheelsets in this way; the diagrams are intended to represent the characteristics of the suspension arrangement when reduced to its bare essentials. What matters is that the stiffer the springs, the more stable the bogie and the faster it will run before reaching its critical speed. Interpreted in more practical terms, to deter hunting, each wheelset must be restrained so that it resists yaw and resists lateral motion relative to the bogie frame.
Figure 20
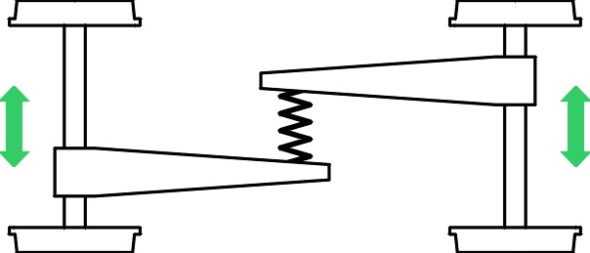
Figure 21
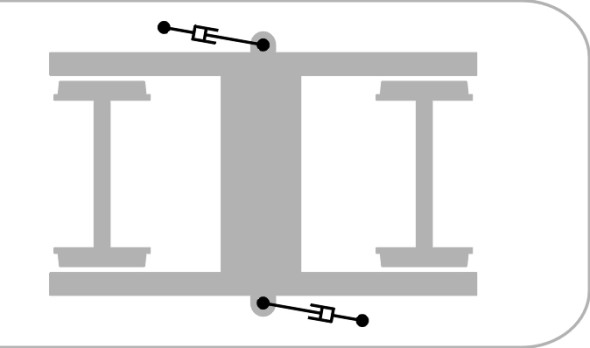
But for steering we want exactly the opposite: low yaw stiffness so that the axles can swivel easily to accommodate a sharp curve, and low lateral stiffness so the axles can move easily from side to side on a reverse curve or a kink in the track. So a compromise is needed. This takes us into difficult territory because any particular vehicle is likely to have several different modes of instability, each arising at a different critical speed. Much painstaking analysis is required to arrive at a workable compromise, involving the use of computer simulation packages and field tests. You will find an authoritative account of the principles involved in [20]. However most solutions have something in common: they exploit the fact that there are two sorts of ‘stiffness’. The first is elastic stiffness, the sort associated with a spring, which provides a resisting force that is proportional to deflection. The second is the sort associated with a damper, which is designed to absorb energy of motion; the resistance is proportional to the rate of deflection. We have already met springs and dampers in a different role: the vertical suspension that transmits the weight of the vehicle to the track beneath, where both are necessary in combination to handle the input from an irregular track surface. Rather than reducing the elastic stiffness of the axle-box bushes, the engineer will look to some form of damping, either in the longitudinal or lateral direction. It turns out that on a railway vehicle, one can use horizontal dampers to resist high-frequency motion of the bogie of the kind that occurs during hunting, where they absorb energy and prevent a build up that can lead to derailment (figure 22). On the other hand, they have less effect on the relatively slow swivelling action of the wheelsets or indeed of the bogie as a whole when it enters a curve.
Figure 22
Steering and track curvature
Using a carefully tailored combination of springs and dampers, it is now possible to design a bogie that will run smoothly at speeds of 350 km/h and above. But high-speed trains don’t steer well on sharp curves, and ideally, they need new tracks whose minimum radius is measured in thousands of metres rather than hundreds as was previously the case. Unfortunately, one cannot always fit shallow curves into a densely populated area, and away from the main line, there will be branch lines, sidings and depots where the alignment is necessarily sub-standard. So let’s try and summarise the factors that determine the minimum radius on which a railway vehicle can operate. We’ll concern ourselves with just two main criteria: passenger comfort and track wear. There is also the question of safety, which we shall deal with separately in the next Section.
Passenger comfort requires among other things that passengers shouldn’t be exposed to forces that might cause them to fall over inside a moving train. As explained in Section R1604, this can be achieved by limiting the centripetal acceleration to about \(0.2 g\), with half compensated by track superelevation or cant, and the remainder uncompensated, leaving a maximum acceleration of \(0.1 g\) (about 1.0 m/s2) parallel to the cabin floor [17]. So we can put
(18)
\[\begin{equation} \frac{V^{2}}{R} \quad = \quad 0.2 g \end{equation}\]where \(V\) is the speed of the train and \(R\) the radius of the curve. With a little rearrangement we can interpret this as a formula for the maximum operating speed consistent with passenger comfort requirements thus:
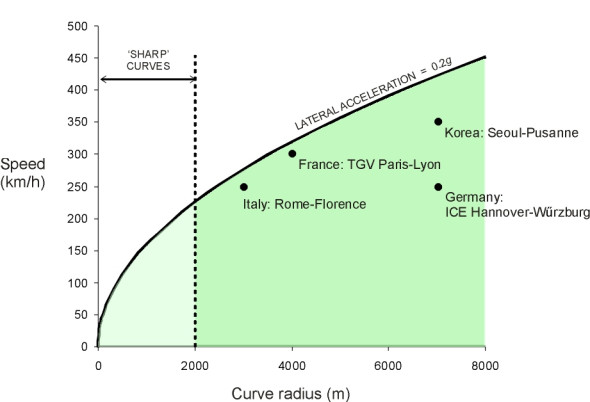
(19)
\[\begin{equation} V \quad = \quad \sqrt {0.2 R g} \end{equation}\]This relationship, which previously appeared in Section R1604, is reproduced here in figure 23. Any point below the black line corresponds to an acceptable combination of track curvature and operating speed. To illustrate how things work out in practice, we have plotted some dots representing the design specification for each of four high-speed railways built during the last three decades [16]. Each lies within the boundary.
Figure 23
But what about the track? When it enters a curve, a high-speed train generates a lateral force that will tend to shift the rails and sleepers bodily sideways across the surface of the underlying ballast. If the lateral acceleration in the plane of the track is limited to \(0.1 g\), consistent with passenger comfort, then for a wheelset carrying a load of 22.5 tonnes the track-shifting force will be \(0.1 \times 22.5 \times 9.81 = 20\) kN approximately. This is in addition to any ‘friction’ flanging force mentioned earlier. It does not take into account random variations, but it is well within the recommended UIC limit of 60 kN. It follows that there is scope for running trains faster without necessarily damaging the track, and this is the rationale adopted by many rail companies who have introduced tilting trains to take advantage of the available margin while maintaining the lateral acceleration for passengers within currently accepted limits. This will form the topic of Section R0410.
Radial steering
Even today, engineers continue to work towards better curving performance, especially for railways and tramways where sharp curves are common. Anything one can do to reduce track wear on the curves will prolong the life of the track and postpone the need for rail replacement together with disruptive closures. The goal is a zero angle of attack, that is to say, radial steering. There are many different ways of doing this, some of which were discovered nearly a century ago. We’ll group them into four main categories.
The first category relates to bogies in which the leading and trailing wheelsets are connected so they can swivel freely relative to the bogie but not independently of each other; such a system is often called ‘self-steering’. The most common version uses diagonal ‘cross-anchors’ or braces. These are often fitted to three-piece bogies and they effectively reduce the bending stiffness of the wheelsets to zero. A variation on this theme is Scheffel’s self-steering bogie, the schematic layout of which is shown in figure 24. It features diagonal spring/damper connections between wheelsets. The second category relates to bogies in which the yaw angles of the wheelsets are determined by the angle of the bogie relative to the vehicle body. In other words, when the bogie swivels on the entry to a curve, a link connected to the body frame directs the axles into a radial alignment (or approximately so). These are termed ‘forced steering’ systems. The schematic layout of a body-driven steering lever arrangement is shown in figure 25. It has been used successfully on the Japanese Railways Hokkaido Series 283 passenger diesel motor units, where tests have shown that it cuts lateral forces on the rail by a half or more [10]. While systems in these first two categories have led to improvements in curving behaviour [7], they have also introduced new forms of instability [27].
Figure 24
Figure 25
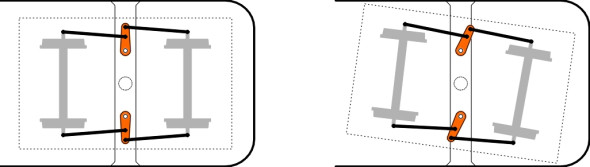
Figure 26
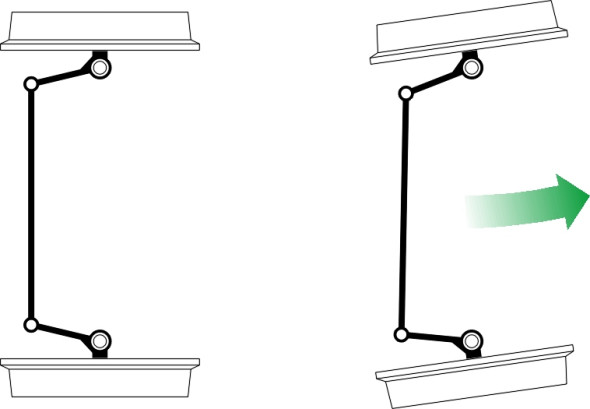
The third category consists of systems where the control input arises not from a mechanical linkage but actuators (hydraulically or electrically driven) connected directly to the wheelsets and widely termed ‘active steering’. They contain sensors that detect incipient accelerations in the vehicle and react quickly, applying forces and displacements that counteract the effects. These are still at an early stage of development. The fourth category brings together some equally radical arrangements in which the two wheels on any given axle rotate independently. It is even possible to mount the wheels on kingpins like the front wheels of a car, which permits a lower cabin floor (figure 26). Unlike conventional systems with a solid axle connection, these arrangements eliminate hunting, but they don’t automatically centre themselves on the track or steer naturally into a curve. The solution is to provide a torque connection between the wheels through electronically controlled hub motors. A review of systems in these last two categories can be found in [6].
Conclusion
If you happen to live near a tramline that passes through a sharp curve, you will hear the flanges squealing from a considerable distance away. It happens on mainline railways too, particularly on tracks where the alignment dates back to the nineteenth century when tracks were woven through densely developed urban areas. There is a notorious curve at London Bridge in the UK, where every train must slow down to a few kilometres per hour as it passes through the station. While the problem of steering on high-speed tracks has largely been resolved using flexible suspension mountings with lateral and longitudinal damping, there remains the challenge of existing tracks with sharp curves where the high rate of wear adds greatly to the costs of operation. Some progress has been made with independently-rotating wheels with sophisticated control systems to damp oscillations, and more developments may be expected within the next few years. Although not obvious to the casual onlooker, they may lead to significant reductions in track maintenance costs that are ultimately reflected in the price of your train ticket.