R.0418
Hunting
‘All guidance measures carry the seeds of their own destruction’
In the coalmines of northern England during the early 1800s, engineers were experimenting with steam-powered locomotives to haul wagons around the mine workings. The opening of the Liverpool-Manchester Railway on 15September 1830 gave them a chance to try out their machines at speed. The results were not impressive: they rumbled unsteadily along the rails, and the wagons they hauled suffered from a bumpy ride. Over the following decades, better quality track and vehicle suspension helped to improve the ride quality and make passenger travel feasible. But as the locomotives became more powerful, a problem emerged that no-one had foreseen. When driven above a certain speed, a vehicle would begin to lurch from side to side, a phenomenon that came to be known as ‘hunting’. The cause was unclear, and with no simple cure in view, until the 1950s hunting was accepted as inevitable [3]. It limited the speed at which a railway train could safely travel, in the same way that the sound barrier limited the speed of an aircraft, except that the threshold varied according to the configuration of the vehicle and the quality of the track. Building on years of research and development, engineers have since discovered how to raise the speed threshold for each generation of high-speed trains.
Klingel motion
At the root of the problem lies a phenomenon that can be understood entirely in terms of geometry. Almost all railway vehicles have conical wheel treads, and since each pair of wheels is connected by a solid axle, the potential for oscillating behaviour is built into every wheelset. The process was first explained by W Klingel in 1883 [6].
Kinematic behaviour
Let’s imagine that the track is perfectly straight, and that the wheelset is centrally aligned on the track, pointing straight ahead with the axle at right angles to the rails. We’ll call this the ‘reference position’. With the wheelset in this position, the rolling radius of the left-hand wheel (the radius from the axle centreline to the centre of the contact patch) will be the same as the rolling radius of the right-hand wheel. Denote the common radius by \(r\). If set in motion from the reference position, the wheelset will roll ahead indefinitely without any deviation from the track centreline. Of course no track is perfectly straight so if you lower a wheelset onto the rails at any point and set it rolling, no matter how carefully aligned at the start, it will soon meet a deviation in the alignment so that it no longer moves parallel with the rails. Figure 1 shows the wheelset pointing at a small angle to the left (in practice it will be no more than a fraction of a degree but the angle is exaggerated in the diagram). We’ll call the left-hand wheel the ‘outer’ wheel and the right-hand wheel the ‘inner’ wheel. Since the wheel treads are conical, the outer wheel will ride up the rail while the inner wheel will descend (figure 2). The rolling radius of the outer wheel will become progressively larger, and as it does so, it will travel further along the rail surface with every revolution. Meanwhile the rolling radius of the inner wheel will become progressively smaller, and the wheel will cover less distance along the rail with every revolution. The result is that the outer wheel speeds up, the inner wheel slows down, and the wheelset as a whole will swivel in a horizontal plane and steer back towards a central position (figure 3). This is what makes a conical wheelset ‘self-steering’, a fundamental characteristic we came across in Section R1610.
Figure 1
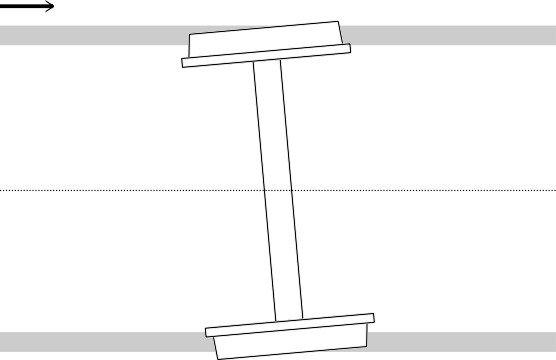
Figure 2
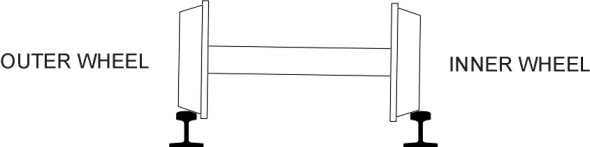
Figure 3
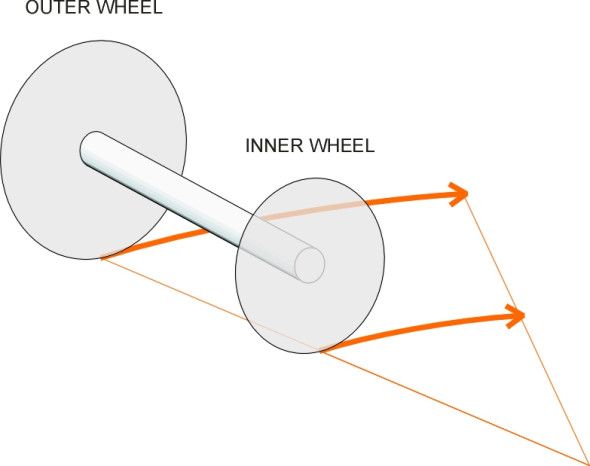
But when the wheelset regains the track centreline it is not pointing straight ahead, so it crosses the centreline and continues to deviate to the opposite side, where the same correction process happens in reverse. The wheelset will continue to oscillate from side to side, echoing the original alignment error. A large initial error will involve larger oscillations, while a small initial error will results in smaller oscillations. Such motions are called kinematic\(\,\) motions as opposed to ‘dynamic’ phenomena because the bodies involved are behaving like rigid mechanical linkages that trace out pre-determined paths in space. There is no slipping, no elastic deformation, and the speed and mass of the vehicle are irrelevant. The deviations must be quite small, because of the limited clearance between each wheel flange and the shoulder of the corresponding rail. Otherwise the flanges will collide with the rails, and the collisions introduce a new phenomenon that we’ll describe later.
To make progress, we must fill in some of the details hinted at in Section R1610. The conical shape of each wheel tread is crucial and as before we’ll denote the ‘half-angle’ or angle of taper by the symbol \(\gamma\). It’s quite small: usually 1:20, or 1:40 for many high-speed lines. A 1:20 taper tells us that the tangent of \(\gamma\)\(\,\) is 1/20 = 0.05, and since for small angles the tangent is approximately equal to the angle itself we have \(\gamma \sim 0.05\) radians. Denote the spacing between the wheels by \(w\); more precisely, this is the distance between the centres of the two contact patches, which we shall approximate via the distance between the rail centrelines, which for standard gauge track is close to 1500 mm.
It’s convenient to define the oscillations in terms of the lateral deviation \(y\) of the centre of the wheelset from the centreline of the track, measured as positive to the left. Because of the limited flange clearance, the range of variation of \(y\) is usually no more than \(\pm\) 8 mm. As shown previously in Section R1610, when the wheelset deviates to the left by a distance \(y\), the rolling radius of the outer wheel increases by an amount approximately equal to \(\gamma y\), and the rolling radius of the inner wheel will fall by the same amount. The changes are approximate because in practice (a) the wheelset will tilt slightly, and (b) the rail surface is curved in cross-section so the centre of contact shifts as the wheelset deviates from side to side. Both affect the geometry, but not very much.
As a result, the wheelset curves to the right along a path of radius \(R\)given by
(1)
\[\begin{equation} R \quad = \quad \frac{wr}{2 \gamma y} \end{equation}\]In broad terms, the smaller the cone angle, the greater the radius of curvature.
Wavelength formula
We’ll now cast equation 1 as a differential equation that can be solved to predict the pattern of oscillations traced out by the wheelset as it roll along the track [1] [14]. If we denote distance moved in the forward direction by \(x\), then by definition, the radius of curvature \(R\) of the path of the wheelset in the \(x\),\(y\) plane satisfies the equation
(2)
\[\begin{equation} \frac{1}{R} \quad = \quad - \frac{d^{2}y}{d x^{2}} \end{equation}\]and substituting for \(R\) via equation 1 leads to the differential equation
(3)
\[\begin{equation} \frac{d^{2}y}{d x^{2}} \;\; + \;\; \frac{2 \gamma }{rw} \cdot y \quad = \quad 0 \end{equation}\]whose solution takes the general form
(4)
\[\begin{equation} y \quad = \quad A \sin kx \;\; + \;\; B \cos kx \end{equation}\]where \(A\), \(B\) and \(k\) are constants. We can determine \(k\) by substituting equation 4 back into equation 3, to find that
(5)
\[\begin{equation} k \quad = \quad \sqrt { \frac{2 \gamma }{rw}} \end{equation}\]From this we can deduce the wavelength \(\lambda\): the distance travelled by the wheelset during one complete oscillation. Since according to equation 4 the lateral deviation goes through a complete cycle when \(k x\) changes from zero to \(2 \pi\),
(6)
\[\begin{equation} \lambda \quad = \quad \frac{2 \pi }{k} \quad = \quad 2 \pi \sqrt {\frac{rw}{2 \gamma}} \end{equation}\]For example, if \(r = 0.5\) m, \(w = 1500\) mm, and \(\gamma = 0.05\) radians, then the wavelength is nearly 17 metres. The constants \(A\) and \(B\) depend on the initial conditions, i.e., the placement of the wheelset at the origin \(x\) = 0. For example, if the wheelset is placed 3 mm to the left of the track centreline and pointing straight ahead, it turns out that \(B\) is zero and the curved traced out is a cosine curve with amplitude \(A = 3\) mm. Hence, the wheelset starts 3 mm to the left and as it rolls forward it returns to its reference position on the track centreline, crosses the centreline, and continues moving to the right until it reaches an extreme deviation of - 3 mm, when it returns and crosses the centreline again, and finally regains its initial position at 3 mm to the left. The complete cycle takes place within a distance of about 17 m (figure 4).
Figure 4

The hunting phenomenon
Passengers are scarcely aware of Klingel motion because at low speeds the oscillations are masked by other disturbances. But experience with all kinds of railway vehicle has shown that when the speed reaches a certain level, the oscillations will get worse. The body will zig-zag from side to side while the wheel flanges collide with the inside shoulders alternately of the left and right rails. The impact not only jolts the passengers but wears out the wheels and track and can lead to derailment. The phenomenon is called ‘hunting’, a term originally applied to the behaviour of control devices that had nothing to do with railways. One of the earliest examples of such a device was the centrifugal governor used by James Watt to regulate the speed of his stationary engines. He attached a set of spring-loaded weights to an output shaft. The weights rotated with the shaft and when the speed of rotation exceeded the target level, they flew out under the influence of centrifugal force and triggered a valve that throttled the steam supply. Rather like a bloodhound casting from side to side to catch a scent, the system tended to oscillate between two states (‘on’ and ‘off’).
What causes hunting
Klingel motion doesn’t explain why hunting should occur only above a certain critical speed. The reason is that the underlying model is incomplete: it assumes that the vehicle body and suspension are perfectly rigid and that the wheels grip the rails without slipping. But as described in Section R1717, their behaviour changes subtly when they begin to roll. If you could grasp an axle while it was rolling and twist it like the handle of a giant corkscrew (figure 5), the wheelset would yaw. Such ‘forced’ yaw produces a slight mismatch between the speed at which the rail flows under the advancing wheel and the speed at which it flows under the retarded wheel. In neither case does the tread register perfectly with the rail surface like a gearwheel rolling along a toothed rack. Instead, it creeps along the surface producing a small relative motion even though the tread grips the rail firmly over most of the contact area. We’ll denote the angle of yaw by the symbol \(\psi\). The wheels can also creep sideways across the rail surface to produce a small lateral displacement \(y\).
Figure 5
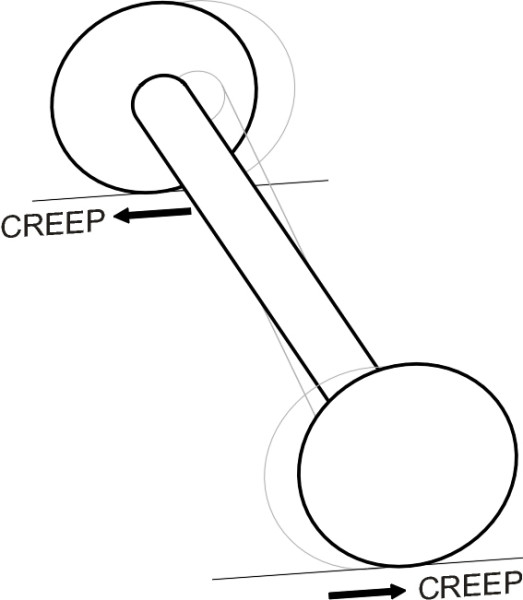
So for a real vehicle there is more freedom for movement than the Klingel model suggests, and we can demonstrate crudely how this leads to hunting by looking at the behaviour of a single wheelset in isolation. The axle-boxes are attached to an imaginary vehicle that holds its position exactly above the centre of the track. The attachments are slightly elastic so the wheelset can shift laterally and yaw relative to its reference position. At the most basic level, the wheelset acts like a mass attached to its suspension springs: when disturbed it will oscillate within the bogie frame. The stimulus is provided initially by Klingel motion, and when the frequency of Klingel motion equals the natural frequency of the wheelset on its springs, the oscillations will grow sharply in magnitude, the ‘extra’ displacements superimposed on the Klingel input, taking advantage of the flexible creep interface between wheel and rail.
However, to predict the motion accurately, we must account for the forces involved and the displacements they produce in closer detail. The movements of the wheelset are governed by two sets of forces: (a) the forces supplied by the suspension springs, which act to restore the wheelset to its central position, and (b) the creep forces, which have a special property. Unlike the force produced by a spring, which is proportional to the deflection, a creep force \(P\) increases or decreases in proportion to the creep rate; in other words, it behaves like the damping force in a vehicle suspension. In the case of a longitudinal creep force the creep rate is defined as the relative speed \(\dot x\) of the wheel tread relative to the rail, expressed as a proportion of the forward speed \(V\) of the vehicle. The constant of proportionality is known as a creep coefficient, denoted by \(f\) (see Section R2019). Thus
(7)
\[\begin{equation} P \quad = \quad f \frac{\dot x}{V} \end{equation}\]Let us now visualise what happens when the wheelset begins to oscillate. Imagine the wheelset aligned dead ahead but displaced laterally to the left by a small distance \(y\) (figure 6). The left-hand wheel has greater rolling radius so it is impelled forward at a slightly higher speed than the right-hand wheel. The right-hand wheel is dragged rearward, with the result that the wheelset yaws to the right. But the rate of yaw is no longer determined solely by geometry: the wheelset must obey Newton’s laws and its motion is governed by its inertial mass (specifically its rotational inertia about a vertical axis) together with the disturbing forces. In figure 6, if the wheel treads are conical, at the starting position, the difference in rolling radius and hence the difference in creep rates will be proportional to the lateral displacement \(y\). In turn, the forces producing yaw will be proportional to \(y\). In other words, the greater the lateral displacement, the greater the forces that cause the wheelset to yaw. Once it begins to yaw, the wheels are no longer aligned parallel with the track so the wheelset is dragged sideways across the rail surface towards the track centreline (figure 7). Again, inertial mass plays a role, but this time it’s the inertia of linear motion rather than rotational inertia. And the creep forces act laterally rather than longitudinally. When the wheelset reaches the track centreline the process is repeated in reverse. Lateral displacement leads to yaw, and conversely, yaw leads to lateral displacement. Mathematically, the two motions are ‘coupled’, and it is the creep forces that provide the link between them.
Figure 6
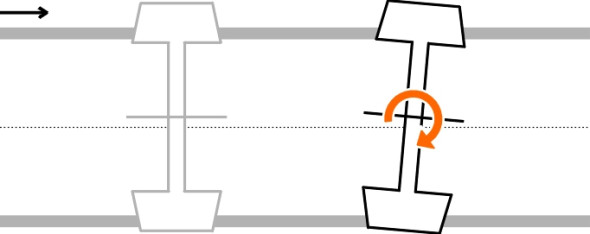
Figure 7
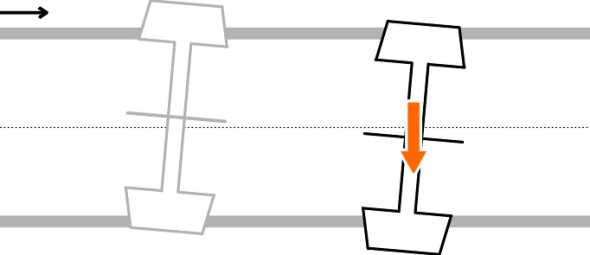
Crucially, the creep forces are affected by the forward speed of the vehicle. When the vehicle is travelling slowly (\(V\) is small) we see from equation 7 that the creep forces are large so the system behaves like a rigid mechanism, and the path followed by the wheelset is close to that predicted by Klingel. But when \(V\) is large they diminish and inertial factors come into play: in crude terms, the wheelset behaves more like a mass attached to a spring. The coupling process can also be visualised as an alternating flow of energy. When a wheelset swivels, it acquires angular momentum together with kinetic energy associated with its rotation about a vertical axis. And likewise, when the wheelset moves laterally it acquires kinetic energy of the kind we associate with straight-line motion. The two motions are synchronised but they occur 180\(^\circ\) out of phase so that energy cycles between the two. Such behaviour can be pictured as a closed-loop feedback process [17]. And the total energy isn’t fixed - it can be augmented from the forward motion of the vehicle, accumulating gradually from one cycle to the next when the vehicle reaches its critical speed.
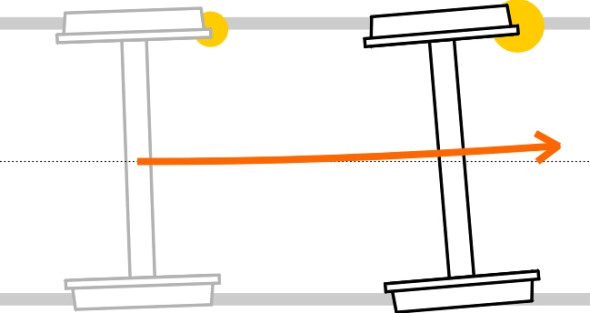
These are the factors that might drive the oscillation of an isolated wheelset if such were to exist. A full mathematical description runs to many pages (see, for example [16]). But it’s a simplified picture. We’ll see in a moment that the whole bogie frame can oscillate and indeed the whole vehicle. And far from being a smooth, continuous process, the oscillation changes abruptly when a wheel flange makes contact with the inner shoulder of the rail. There is a sudden jolt, and the colliding wheel is dragged rearward relative to its partner, thereby causing the wheelset to yaw towards the impacted rail in such as way as to exacerbate the impact (figure 8). Afterwards the wheelset rebounds in the opposite direction and the opposite wheel strikes the other rail. This is the condition that railway engineers describe as ‘hunting’, and it is one that the passengers certainly notice.
Figure 8
Theoretical models
During the nineteenth century, railway engineers were anxious to reduce the journey times between railway stations but were faced with severe hunting problems whenever the vehicle speed rose above a certain level. Solving the problem wasn’t simply a question of trial-and-error (experiments with real trains are expensive and you can’t tinker blindly with the suspension and hope that the train won’t derail during the next high-speed test). What was needed was a theoretical understanding of the hunting process that would throw a spotlight on the key variables - the variables that must be changed to achieve a practical solution. But the task of putting the equations together and solving them called for patience, perseverance, and a gifted mathematician. It was almost a hundred years after the first steam railways were built that anyone really understood how to do it. The process took place in three stages, and the story has been well described in [2] and [23].
The first step was to model the relationship between the creep forces and deflections that occurred during rolling contact. An early breakthrough in this area was made in 1916 by F W Carter, a mathematician-turned-engineer, whose contribution we met earlier in Section R2019.
The second step was to formulate the equations of motion that describe the behaviour of the system as a whole. They take the form of simultaneous equations, one for each ‘degree of freedom’. A degree of freedom represents one particular direction of movement for an element of the system. A vehicle may contain several elements such as a bogie frame, a wheelset, or a wagon body, and any given element may be capable for movement in more than one direction. Each equation is constructed by listing all the forces that act in the direction concerned including the d’Alembert force (mass times acceleration), for the element in question. Although the results look rather forbidding, in principle this is not a difficult thing to do. For example, a single wheelset can move from side to side (in the \(y\) direction) and it can also yaw about a vertical axis, represented by the angle \(\psi\). Here, there are just two degrees of freedom and two simultaneous equations, whose terms contain derivatives of \(y\) and \(\psi\). We won’t set out the equations here, but you can find the details in [18]. There are also various parameters that appear as constant coefficients including the wheel load, mass, moment of inertia, stiffness coefficients, wheel radius, track width between contact points, and vehicle speed [29]. They don’t affect the underlying nature of the equations, which, because there are only two degrees of freedom, can be solved analytically. There is a further proviso, that the equations are linear in \(y\) and \(\psi\), meaning that the deflections are proportional to the applied forces and vice versa. This is normally the case for small oscillations but as we shall see later, it breaks down when there is flange contact of the kind that occurs during a fully-developed hunting process. So much for the single wheelset. For a two-axle vehicle, things get more complicated. There are three separate elements each of which can yaw and deflect independently: the chassis and the two wheelsets. There is also the question of body roll, which brings the tally to seven independent variables and therefore seven simultaneous equations. As you can imagine, for a vehicle with two bogies each having two sets of suspension (primary and secondary) each of which can deflect independently, the number of variables and therefore the number of equations rapidly multiplies.
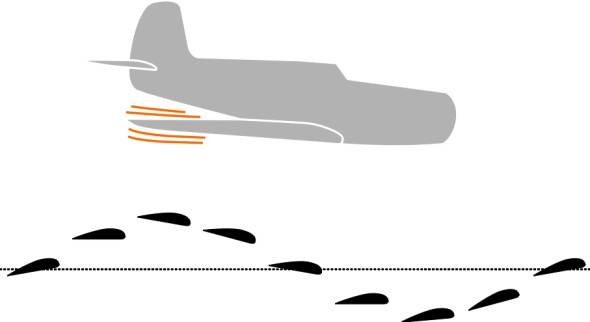
The third step was to find numerical solutions that would show how the parameter values affect the critical speed. This would effectively tell the designer how to configure a high-speed bogie. It was not an easy task, because the calculations could only be done by hand, perhaps with help from an analogue computer, the only kind that was available at the time. However, it was eventually realised that the hunting problem is similar to another problem that occurs in the field of aeronautics. Known as ‘flutter’, it is caused by the elasticity of an aircraft wing when buffeted by aerodynamic forces. A wing is slightly flexible, and like a plank of wood clamped at one end - say a diving board jutting out over a pool - it can deflect either by bending up and down, or by twisting about its principal axis. Indeed, the wing can oscillate in both senses at the same time. Depending on its weight distribution and the structural stiffness of the wing in bending and torsion, an upward deflection may cause the leading edge to twist downwards, and the reduced angle of attack leads to an abrupt reduction in lift. The wing then deflects downwards which in turn causes the twist to reverse so the leading edge rises. As the angle of attack increases so does the lift force and wing bends upwards again (figure 9). The oscillations can increase in severity fed by a continual input of energy from the fluctuations in air pressure across the wing surfaces.
Figure 9
Flutter tends to arise abruptly at a certain critical speed, and during the early years of the last century it destroyed many aircraft. The phenomenon is very similar to the oscillation of a railway wheelset: it involves two coupled motions that exchange energy between them, with the potential for accumulating energy so that the amplitude grows until the wing breaks. In fact, the linear equations of motion of a railway vehicle and the equations for aircraft wing flutter have a similar form [27], and historically, the solution of hunting on railways drew heavily on specialists who had worked in the aircraft field so they were able to simplify the equations on the basis of experience.
Simplifying the equations is one thing; solving them is another. In the case of a perfectly conical wheelset rolling in isolation along the track, for small displacements the equations are linear and can be solved to yield a formula for the critical speed in terms of the wheel geometry, creep coefficients, and other key parameters. You can find the formula in [19]. But to deal with more a realistic case where the wheels are worn and they deflect over a large range with flange contact, one must resort to computer simulation [10] supported by laboratory experiments on a roller test rig [28]. It was through such efforts that engineers were able to identify the variables that mattered most and thereby arrive at a bogie design that was stable at high speeds. We’ll try to summarise the results in a moment, but first let’s picture the kinds of oscillation the engineers were looking for. It’s not just the wheelset that can oscillate, but at a higher level, the bogie frame and the vehicle body.
Modes of instability
A railway vehicle is built up from several elements namely the wheelsets, two bogie frames, and the vehicle body. They can all move relative to one another. The movements may be small, but since each element has inertial mass and is connected to its neighbours effectively by springs, each has the potential to oscillate at its own natural frequency. The equations of motion can be difficult to handle even with a digital computer. But from a practical point of view, the most important modes of behaviour occur when the natural frequencies of two neighbouring elements such as a wheelset and bogie frame are in a simple numerical ratio, because the one can stimulate the other. The oscillations then become synchronised and escalate rapidly in size.
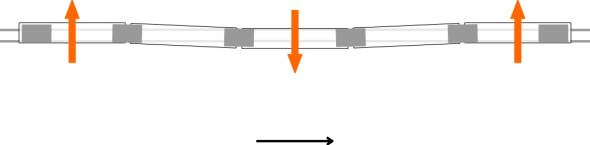
Such patterns of behaviour can be predicted at least in outline from a relatively simple equation known as the characteristic equation\(\,\) distilled from the equation of motion. The roots of this equation, known as the eigenvalues, effectively map out the unstable modes [15]. This was how the Japanese pioneer Matsudaira discovered that a two-axle bogie was vulnerable to two hunting motions: ‘primary’ and ‘secondary’. Primary hunting occurs at a lower speed and affects the whole bogie frame. Secondary hunting occurs at the level of the individual wheelset [7]. Both can occur simultaneously, and some special cases are pictured in [20]. If we think of a bogie as a vehicle in its own right this picture applies to any two-axle vehicle such as an old-fashioned freight wagon. Figure 10 shows one particular case in simplified form: the wagon veers first in one direction and then the other as it shifts from side to side across the track. The motion of a passenger coach is more complicated because there are two bogies, and the body is mounted on secondary suspension springs that confer additional degrees of freedom. The body can also roll about a longitudinal axis as shown in figure 11, a motion sometimes referred to as ‘sway’ [11], and other modes are possible for articulated vehicles [12]; one is shown in figure 12.
Figure 10

Figure 11
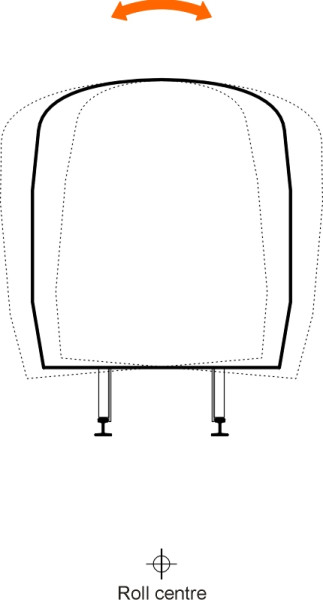
Figure 12
The stable bogie
Over the years, mathematical analysis backed by roller rig testing has revealed combinations of suspension parameters that lead to stable running. Today, trains move routinely at 350 km/h with no sign of hunting, an outcome that would have seemed improbable a hundred years ago. There are two distinct strategies that have so far been found to work quite well [21].
The first applies to bogies, which have a relatively short wheelbase [25]. The breakthrough was made during the 1950s in Japan. Matsudaira, who had previously been involved with flutter problems on military aircraft such as the Zero, reasoned that stiffness in lateral displacement and yaw was the key to a successful bogie design. Without the aid of a computer, he established the required parameter values for a 2-axle bogie and tested new configurations on a roller rig. They formed the basis of the bogie design for the Shinkansen Tokaido line that opened for service in 1964 [3] [24]. In addition, the half-cone angle was reduced from 1:20 to 1:40, which contributed towards raising the critical speed, but had a less fortunate side-effect, which was to restrict the ability of trains to steer round sharp curves. However this did not matter because the Tokaido line was a new railway built on a completely a new alignment. On the other hand, a shallow half- cone angle makes the wheelset more sensitive to wear - it must be re-profiled at relatively frequent intervals.
The second strategy was developed in Britain during the 1960s. It was needed urgently to halt the growing number of derailments of 2-axle freight wagons that accompanied the general rise in speeds following modernisation of the national network. Led by A H Wickens, who had a background in aeronautical engineering, the research team formulated the equations of motion. There were seven simultaneous differential equations involving lateral displacement and yaw of the wheelsets and the car body, together with roll of the car body [26]. Building on Matsudaira’s work, the researchers solved the equations through a combination of (a) simulation using analogue computers, (b) numerical solutions obtained from a digital computer, and (c) analytical techniques [4] [24]. The results differed from Matsudaira’s because the freight wagon has a much longer wheelbase than a bogie, and the wheelbase affects the critical hunting modes. The solution was a relatively flexible suspension with lateral damping to eliminate body instability [22]. This pushed up the critical speed to 225 km/h.
The results were later transferred to passenger coaches for the first generation of British high speed trains [4], and before the HST finally went into service in 1977, the design was modified and tested over a total distance of 400 000 km [8]. The ride was smooth, and with hunting eliminated, the rails and tyres were less prone to wear. In particular, the tyres would last for 180 000 km before the vehicle had to be taken out of service for re-profiling, the equivalent of 6 months in regular service.
Conclusion
Experience has shown that the hunting problem can be deferred so that a railway train will run smoothly and safely at speeds of more than 350 km/h. All you need is a carefully maintained track, regular re-profiling of the wheels, and careful design of the bogie suspension with stiff springs or stiff dampers to restrain yaw and lateral displacement. But as hinted earlier, these measures carry a penalty. Increasing the stiffness of the primary suspension impairs the ability of the wheelset to swivel and to shift from side to side to accommodate sharp curves or irregularities in the geometry of the track. In other words, it doesn’t steer very well. In the next section, we shall take a closer look at the steering problem. It turns out [9] [13] that you can make a vehicle run fast on straight track without hunting, or you can make it go round sharp curves without de-railing, but achieving both at the same time is more difficult.